The Hardening Soil with
small strain stiffness model is implemented by using the
Modified Mohr-Coulomb model and Small strain overlay model,
and needed two additional parameters as below:
G0ref |
: Initial
or very small-strain shear modulus |
Threshold
strain (γ0.7) |
: Shear strain
at which the shear modulus is about 70% of the
initial small-strain shear modulus |
The strain range
in which soils can be considered truly elastic is very
small. With increasing strain range, soil stiffness decrease
nonlinearly as the following graph.
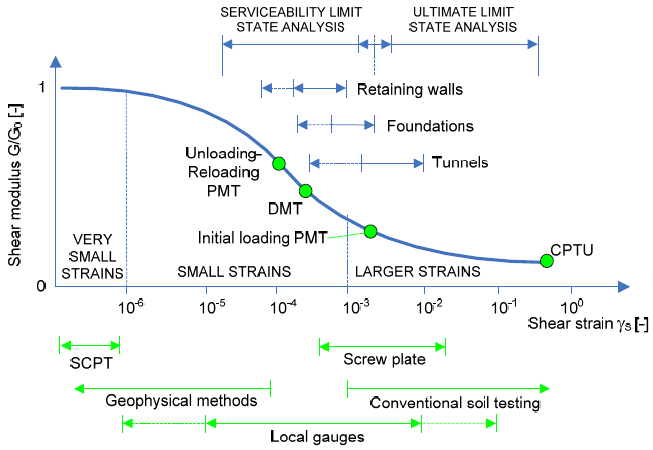
To reflect the above
characteristics, the Hardening Soil with small strain
stiffness model uses the modified Hardin & Drnevich
relationship as the following equation.
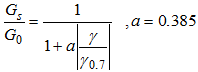
Gs |
: Shear modulus |
G0 |
: Initial shear modulus |
γ |
: Shear strain |
γ0.7 |
: Shear strain at which
the shear modulus is about 70% of the initial
small-strain shear modulus |
[Nonlinear
Parameters]

Following is the
summary of parameters for the Hardening Soil (small strain
stiffness) model.
Parameter |
Description |
Reference value
(kN, m) |
Soil stiffness and
failure |
E50ref |
Secant
stiffness in standard drained triaxial test |
Ei x (2 – Rf) /2
(Ei = Initial stiffness) |
Eoedref |
Tangent
stiffness for primary oedometer loading |
E50ref |
Eurref |
Unload
/ reloading stiffness |
3 x E50ref |
m |
Power
for stress-level dependency of stiffness |
0.5 ≤ m ≤ 1 (0.5
for hard soil,
1 for soft soil) |
C |
Effective cohesion |
Failure parameter
as in MC model |
φ |
Effective friction
angle |
Failure parameter
as in MC model |
ψ |
Ultimate dilatancy
angle |
0 ≤ ψ
≤ φ |
Advanced parameters
(Recommend to use Reference value) |
Rf |
Failure Ratio (qf
/ qa) |
0.9 (< 1) |
Pref |
Reference pressure |
100 |
K0NC |
K0 for normal consolidation |
1-sinφ
(< 1) |
Tensile strength |
Cut
off value for tensile hydrostatic pressure |
- |
Small
strain stiffness |
Threshold
Shear
strain |
Shear strain
at which shear modulus has decayed
to 70% of initial shear
stiffness (G0ref) |
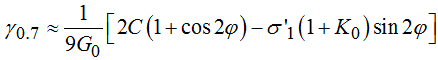
|
β |
Shear
modulus at small strain |
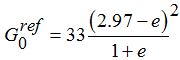
|
1. Relation
of principal stress with principal deformations in HSS.
The Hardening Soil results for strains are generated using
return mapping algorithm as shown below:
The nomenclature follows a rule for
GTS NX program.
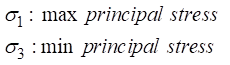
The hyperbolic equation in the “Schanz
& Vermeer” paper is modified to accommodate the nomenclature.
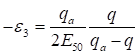

The following equations come from
return mapping algorithm, and these equations are for
tri-axial or oedometer conditions
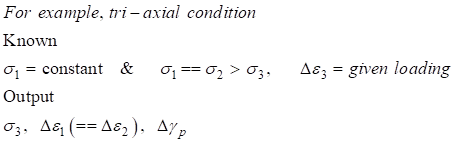
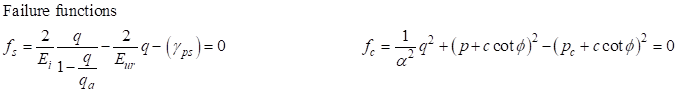
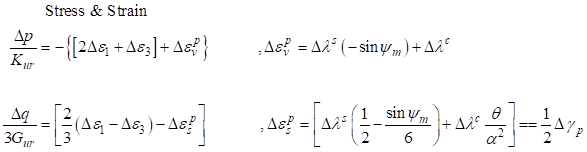
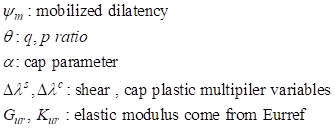
The plastic multiplier variables
are determined using a given loading. |



