General Material (Behavioral properties)

 

▒ Concrete Damaged Plasticity

The concrete damaged plasticity model provides a general capability for modeling concrete and other quasi-brittle materials, i.e. rock, mortar, ceramics in all types of structures and is designed for applications in which concrete is subjected to dynamic loading due to earthquake under low confining pressures. This model is not suitable for concrete under high confining pressures which would lead to ductile behavior. This model can describe the irreversible damage that occurs during the fracturing process of concrete under relatively low confining pressures. Using this model, the following behaviors of concrete can be described.

  • Different behaviors for tension and compression. (Failure tensile stress and ultimate compressive stress)

  • Different reductions of the elastic stiffness when unloading for tension and compression.

  • Stiffness recovery effects during cyclic load reversals

 

 

Parameters

Dilation Angle & Eccentricity

The concrete damaged plasticity model assumes non-associated potential plastic flow. The flow potential G used for this model is the Drucker-Prager hyperbolic function.

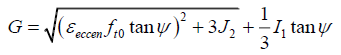
fb0/fc0 ratio

fb0: the initial equibiaxial compressive yield stress

fc0: the initial uniaxial compressive yield stress

Kc

The ratio of the second stress invariant on the tensile median to that on the compressive meridian at initial yield

Viscosity Parameter

Material models exhibiting softening behavior and stiffness degradation often lead to convergence difficulties. This can be overcome through the viscoplastic regularization by permitting stresses to be outside of the yield surface. The viscoplastic regularization for the concrete damaged plasticity model can be realized by applying Duvaut-Lions model. The viscosity parameter represents the relaxation time of the viscoplastic system.

 

Stiffness Recovery

Tension Recovery

Tension recovery is set equal to 0 by default. This means the tensile stiffness is not recovered as the load changes from compression to tension once crushing micro-cracks have developed.

Compression Recovery

Compression recovery is set equal to 1.0 by default. This means the compressive stiffness is recovered upon crack closure as the load changes from tension to compression.

 

Concrete Damaged Plasticity Function

Compression Hardening Curve

Define hardening data in terms of an inelastic strain.

Compression Damage Curve

Define damage curve in terms of an inelastic strain. The damage parameter is deduced from a material test with ramped loading/unloading cycles as follows:

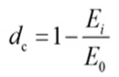
Tension Softening Curve

Define softening data in terms of an inelastic strain.

Tension Damage Curve

Define damage curve in terms of an inelastic strain. The damage parameter is deduced from a material test with ramped loading/unloading cycles as follows:
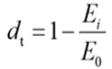