 Revision of Ver.7.4.1
Revision of Ver.7.4.1 Revision of Ver.7.4.1
Revision of Ver.7.4.1Function
Create elements.
Call
From the Main Menu select Model > Elements > Create Elements.
Select Geometry > Elements > Create in the Menu tab of the Tree Menu.
Click .jpg) Create Elements in the Icon Menu.
Create Elements in the Icon Menu.
Shortcut key: [Alt]+1
Entry
|
|
Click to the right of Create Elements: Display the Element Table Start Node NumberAssign a number to the new starting node created together with new elements in the Model Window. This number is auto-set to the largest node number in use +1. To modify this item, click and select an option to specify a desired number. Start Element NumberAssign a new starting element number. This number is auto-set to the largest element number in use +1. To modify this item, click and select an option to specify a desired number.
Element TypeAssign an element type and enter additional data. Truss: Truss Element Tension-only/Hook/Cable: Tension-only Elements Compression-only Truss Allow. Comp : Allowable maximum compressive force Tens. Limit : Allowable tensile force used in the process of iterative analysis For tension-only elements, Allow Comp. is assigned 0 and Tens. Limit is checked off generally. If Tens. Limit is checked on and a specific value is entered, the element no longer resists forces exceeding the Tens. Limit, and the excess forces will be transferred to neighboring elements. Hook If a displacement takes place beyond the Hook Distance, the element starts resisting tension CableEnter the ratio of unstrained length of unstrained length to element length (Lu/L) and the Pretension load additionally. "Cable Element" is auto-converted into equivalent Truss Element in the case of a linear analysis and Elastic Catenary Element in the case of a geometric nonlinear analysis. Generate a Cable Element and introduce Tension Force at the same time. Lu: Enter the unstrained length of Cable (Lu), which will indirectly adjust element stiffness and tension force from element length. (Lu: Unstrained length of Cable, L: Element length) If Lu/L>1, the cable is sagging and reduced stiffness is applied. If Lu/L<1, the distance between the two nodes is longer than the unstrained length, and it has an effect of introducing a tension force. Pretension: Enter the Pretension load to be introduced to Cable. Horizontal: Enter the Horizontal pretension load, which will be automatically converted into the pretension load to be introduced to Cable. Entered pretension is applied only when nonlinear analysis is performed. Unless geometric nonlinear analysis is performed, the entered pretension will be ignored. For linear analysis, pretension should be entered using Load>Prestress Loads> Pretension Loads.
Compression-only/Gap: Compression-only Elements Compression-only Truss Allow. Tens : Allowable maximum tensile force Comp. Limit : Allowable compressive force used in the process of iterative analysis For compression-only elements, Allow Tens. is assigned 0 and Comp. Limit is checked off generally. If Comp. Limit is checked on and a specific value is entered, the element no longer resists forces exceeding the Comp. Limit, and the excess forces will be transferred to neighboring elements. Gap If a displacement takes place beyond the Gap Distance, the element starts resisting compression. Note Usage tip of Tension-only/Compression-only element These elements are generally used for modeling members that exert axial forces only such as space trusses, cables and diagonal members as well as for modeling contact surfaces. For example, truss elements resisting axial tension and compression forces can be used to model a truss structure. Tension-only elements are suitable for modeling cables whose sagging effects can be neglected and for modeling diagonal members that are incapable of transmitting compression forces due to their large slenderness ratios, such as wind bracings. Compression-only elements can be used to model contact surfaces between adjacent structural members and to model ground support conditions taking into account the fact that tension forces cannot be resisted. Pretension loads can be used when members are prestressed.
Because these elements do not retain rotational degrees of freedom at nodes, Singular Errors can occur during the analysis at nodes where they are connected to the same type of elements or to elements without rotational d.o.f. MIDAS/Gen prevents such singular errors by restraining the rotational d.o.f. at the corresponding nodes. If they are connected to beam elements that have rotational degrees of freedom, this restraining process is not necessary. As shown in <Figure 1>, you should exercise caution not to induce unstable structures when only truss elements are connected. The structure shown in <Figure 1> (a) lacks rotational stiffness while being subjected to an external load in its plane, resulting in an unstable condition. <Figure 1> (b) and (c) illustrate unstable structures in the loading direction (X-Z plane), even though the structures are stable in the Y-Z plane direction. You should use tension-only and compression-only elements with care. Element stiffness may be ignored in the analysis depending on the magnitudes of loads; e.g., when compression loads are applied to tension-only elements.
(a) When a force is applied in the X-direction on the X-Z plane
(b) When a force is applied in the X-direction perpendicular to the Y-Z plane
(c) When a force is applied in the X-direction perpendicular
to the Y-Z plane <Figure 1> Typical examples of unstable structures that are composed of truss (tension only & compression only) elements General beam/Tapered Beam: Beam Element/Non-prismatic Beam Element Note In-span concentrated loads, distributed loads, temperature gradient loads and prestress loads can be applied to beam elements. A beam element has 6 d.o.f. per node reflecting axial, shear, bending and torsional stiffness. When shear areas are omitted, the corresponding shear deformations of the beam element are ignored. The beam element is formulated on the basis of the Timoshenko beam theory (a plane section initially normal to the neutral axis of the beam remains plane but not necessarily normal to the neutral axis in the deformed state) reflecting shear deformations. If the ratio of the section depth to length is greater than 1/5, a fine mesh modeling is desirable because the effect of shear deformations becomes significant. The torsional resistance of a beam element differs from the sectional polar moment of inertia (they are the same for circular and cylindrical sections). You are cautioned when the effect of torsional deformation is large, as the torsional resistance is generally determined by experimental methods. Beam and truss elements are idealized line elements, thus their cross-sections are assumed to be dimensionless. The cross-sectional properties of an element are concentrated at the neutral axis that connects the end nodes. As a result, the effects of panel zones between members (regions where columns and beams merge) and the effects of non-alignment of neutral axes are not considered. In order for those nodal effects to be considered, the beam end offset option or geometric constraints must be used. The tapered section may be used when the section of a member is non-prismatic. It may be desirable to use a number of beam elements to model a curved beam. When members are connected by pins or slotted holes (<Figure 2> (a) and (b)), the Beam End Release option is used. Note that a singularity error can result in a case where a particular degree of freedom is released for all the elements joining at a node, resulting in zero stiffness associated with that degree of freedom. If it is inevitable, a spring element (or an elastic boundary element) having a minor stiffness must be added to the corresponding d.o.f.
(a) Pin connection
(b)
Slot-hole connection
(d) When elements having different d.o.f. are connected <Figure 2> Examples of end-release application Plate: Plate Element Thick: Thick plate element Thin: Thin plate element With Drilling DOF: To consider the degree of freedom about the perpendicular direction to the plate Note Usage Tip of Plate Element Note
1 Note
2 Pressure loads can be applied to the surfaces of the elements in either the GCS or ECS. A plate element can be either quadrilateral or triangular in shape where its stiffness is formulated in two directions, in-plane direction axial and shear stiffness and out-of-plane bending and shear stiffness. The out-of-plane stiffness used in MIDAS/Gen includes two types of elements, DKT/DKQ (Discrete Kirchhoff elements) and DKMT/DKMQ (Discrete Kirchhoff-Mindlin elements). DKT/DKQ were developed on the basis of the Kirchhoff Thin Plate theory. Whereas, DKMT/DKMQ were developed on the basis of the Mindlin-Reissner Thick Plate theory, which results in superb performances on thick plates as well as thin plates by incorporating appropriate shear strain fields to resolve the shear-locking problem. The in-plane stiffness of the triangular element is formulated in accordance with the Linear Strain Triangle (LST) theory, whereas the Isoparametric Plane Stress Formulation with Incompatible Modes is used for the quadrilateral element. The user may separately enter different thicknesses for an element for calculating the in-plane stiffness and the out-of-plane stiffness. In general, the self-weight and mass of an element are calculated from the thickness specified for the in-plane stiffness. However, if only the thickness for the out-of-plane stiffness is specified, they are calculated on the basis of the thickness specified for the out-of-plane stiffness. Similar to the plane stress element, the quadrilateral element type is recommended for modeling structures with plate elements. When modeling a curved plate, the angles between two adjacent elements should remain at less than 10? Moreover, the angles should not exceed 2~3?in the regions where precise results are required. It is thus recommended that elements close
to squares be used in the regions where stress intensities are expected
to vary substantially and where detailed results are required.
<Figure 3> Example of plate elements used for a circular or cylindrical modeling
Plane Stress: Plane Stress Element With Drilling DOF: To consider the degree of freedom about the perpendicular direction to the plat Note Usage Tip of Plane Stress Element Note The plane stress element may retain a quadrilateral or triangular shape. The element has in-plane tension, compression and shear stiffness only. Quadrilateral (4-node) elements, by nature, generally lead to accurate results for the computation of both displacements and stresses. On the contrary, triangular elements produce poor results in stresses, although they produce relatively accurate displacements. Accordingly, you are encouraged to avoid triangular elements at the regions where detailed analysis results are required, and they are recommended for the transition of elements only (<Figure 4>). Singularity errors occur during the analysis process, where a plane stress element is joined to elements with no rotational degrees of freedom since the plane stress element does not have rotational stiffness. In MIDAS/Gen, restraining the rotational degrees of freedom at the corresponding nodes prevents the singularity errors. When a plane stress element is connected to elements having rotational stiffness such as beam and plate elements, the connectivity between elements needs to be preserved using the rigid link (master node and slave node) option or the rigid beam element option. Appropriate aspect ratios for elements may depend on the type of elements, the geometric configuration of elements and the shape of the structure. However, aspect ratios close to unity (1:1) and 4 corner angles close to 90?are recommended. If the use of regular element sizes cannot be achieved throughout the structure, the elements should be square shaped at least at the regions where stress intensities are expected to vary substantially and where detailed results are required. Relatively small elements result in better convergence.
<Figure 4> Crack modeling using quadrilateral/triangular elements Plane Strain: 2-D Plane Strain Element Note Pressure loads can be applied normal to the perimeter edges of the plane strain element. Because this element is formulated on the basis of its plane strain properties, it is applicable to linear static analyses only. Given that no strain is assumed to exist in the thickness direction, the stress component in the thickness direction can be obtained through the Poisson's effect. The plane strain element may retain a quadrilateral or triangular shape. The element has in-plane tension, compression and shear stiffness, and it has tension and compression stiffness in the thickness direction. Similar to the plane stress element, quadrilateral elements are recommended over the triangular elements, and aspect ratios close to unity are recommended for modeling plane strain elements. Refer to "plane stress element" Axisymmetric: 2-D Axisymmetric Element Note Pressure loads can be applied normal to the circumferential edges of the axisymmetric element. Because this element is formulated on the basis of its axisymmetric properties, it is applicable to linear static analyses only. It is assumed that circumferential displacements, shear strains and shear stresses do not exist. Similar to the plane stress element, quadrilateral elements are recommended over the triangular elements, and aspect ratios close to unity are recommended for modeling axisymmetric elements. Refer to "plane stress element" Solid: 3-D Solid Element Note Pressure loads can be applied normal to the surfaces of the elements or in the X, Y, and Z-axes of the GCS. The use of hexahedral (8-node) elements produces accurate results in both displacements and stresses. On the other hand, using the wedge (6-node) and tetrahedron (4-node) elements may produce relatively reliable results for displacements, but poor results are derived from stress calculations. It is thus recommended that the use of the 6-node and 4-node elements be avoided if precise analysis results are required. The wedge and tetrahedron elements, however, are useful to join hexahedral elements where element sizes change. Solid elements do not have stiffness to rotational d.o.f. at adjoining nodes. Joining elements with no rotational stiffness will result in singular errors at their nodes. In such a case, MIDAS/Gen automatically restrains the rotational d.o.f. to prevent singular errors at the corresponding nodes. When solid elements are connected to other elements retaining rotational stiffness, such as beam and plate elements, introducing rigid links (master node and slave node feature in MIDAS/Gen) or rigid beam elements can preserve the compatibility between two elements. An appropriate aspect ratio of an element may depend on several factors such as the element type, geometric configuration, structural shape, etc. In general, it is recommended that the aspect ratio be maintained close to 1.0. In the case of a hexahedral element, the corner angles should remain at close to 90¡Æ It is particularly important to satisfy the configuration conditions where accurate analysis results are required or significant stress changes are anticipated. It is also noted that smaller elements converge much faster.
Wall: Wall Element In case of Wall,
the wall combination number is additionally entered. Check(
|
Material
Select a material property number, or select a material property name provided that the material property data have been already defined.
No.: Type in a number on the keyboard or use the mouse to enter the number.
Name: Select a material property name.
Click to add, inquire, modify or delete material property data. Material properties can be entered either before or after creating elements.
Select a section (thickness) number, or select a section(thickness) name provided that the section (thickness) data have been already defined.
No.: Type in a number on the keyboard or use the mouse to enter the number.
Name: Select a section (thickness) name.
Click to add, inquire, modify or delete section (thickness) data. Section data can be entered either before or after creating elements.
When elements are of a line type (Truss, Beam, etc.), Beta Angle or the coordinates of Reference Point are specified to define the orientation of sections.
If the coordinates of the Reference Point are entered, MIDAS/Gen internally computes the angle of the point and enters the angle as a Beta Angle automatically.
If the coordinates of the Reference Vector
are entered, z-axis of an element is placed on the plane containing the
Vector.
MIDAS/Gen uses the Beta Angle (¥â) conventions to identify the orientation
of each cross-section. The Beta Angle relates the ECS to the GCS. The
ECS x-axis starts from node N1 and passes through node N2 for all line
elements. The ECS z-axis is defined to be parallel with the direction
of “I?dimension of cross-sections. That is, the y-axis is in the strong
axis direction. The use of the right-hand rule prevails in the process.
If the ECS x-axis for a line element is parallel with the GCS Z-axis, the Beta angle is defined as the angle formed from the GCS X-axis to the ECS z-axis. The ECS x-axis becomes the axis of rotation for determining the angle using the right-hand rule. If the ECS x-axis is not parallel with the GCS Z-axis, the Beta angle is defined as the right angle to the ECS x-z plane from the GCS Z-axis (See below).
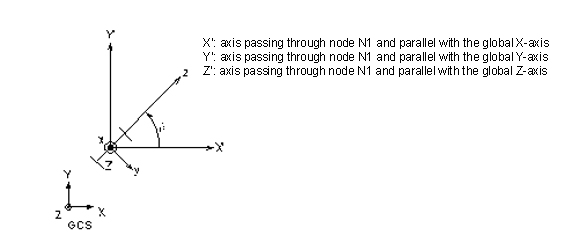
(a) Case of vertical members (ECS x-axis is parallel with
the global Z-axis)
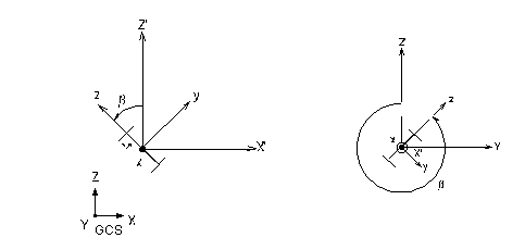
(b) Case of horizontal or diagonal members (ECS x-axis is not parallel with the global Z-axis.)
Beta Angle Conventions
 Nodal Connectivity
Nodal ConnectivityEnter the node numbers defining the element in accordance with the (N1, N2,...) sequence shown in the figure that appears upon selecting Element Type.
Use the following two methods to enter the element's nodal connectivity.
Type in the node numbers in the Nodal Connectivity field.
Click the Nodal Connectivity field, which will turn the background color to pale green. Then, assign consecutively the desired node points in the Model Window to enter elements. If there is no node at the assigned point, a new node is created. It is quite convenient to create elements when Point Grid (or Line Grid) , Grid Snap, Node Snap and Elements Snap. are activated.
If Ortho option is selected the mouse cursor snaps to the entities only in the directions parallel to the currently active coordinate axes (UCS or GCS) from the first point selected.
The nodal locations defining the new elements are entered by directional axes, relative distances or element lengths/angles.
x,y,z: The coordinates of the connecting point of an element are entered in the data entry field, then press the enter key on the keyboard or click .
dx, dy, dz: Enter a distance relative to the reference point and press the enter key on the keyboard or click , If characters are included in the string of numerical values, MIDAS/Gen recognizes them as a relative distance, irrespective of which one of the three methods of data entry is selected
Example: '0,20,10' of ' dx, dy, dz' are expressed as '@10, 20, 10' .
l, theta: l represents the length of an element. Theta represents the angle by which the element direction is rotated with respect to x-axis of the current coordinate system. Once the data are entered, press the enter key on the keyboard or click .
If characters, '@' and/or '<' are included in the string of numerical values, MIDAS/Gen recognizes the numbers as l and theta, irrespective of which one of the three methods of data entry is selected.
Example: '10, 15' of 'l, theta' are expressed as '@10<15'
Note
The origin of the current coordinate system is assigned as the reference
point initially. Subsequently, the last point used becomes the reference
point. To confirm the location of the reference point, enter '@0' in the
data field and press the Enter key on the keyboard.
If Intersect Node is selected and existing nodes are on the element, the element is divided at the existing nodal positions irrespective of the element type.
If Intersect Element is selected and the line element created intersects with an existing line elements, nodes are automatically created and the line elements are divided at the intersections.
If Create Intersecting Nodes is selected and even if there are no interior nodes in the created plate and solid elements, nodes are created at the intersections of the lines extended by the exterior nodes and plate or solid elements are subsequently created.