Revision of Ver.7.4.1 Revision of Ver.7.4.1Function
Add, modify or delete the properties of general link elements.
General Link elements are used for modeling damping devices, base isolators, compression or tension-only elements, plastic hinges, soil springs, etc. General Link elements can be assigned linear and nonlinear properties using spring properties.
Revision of Ver.7.4.1The procedure for boundary nonlinear dynamic analysis is shown below.
|
Procedure |
Menu |
|
1. Define material properties |
Model>Properties>Material... |
|
2. Define section properties |
Model>Properties>Section... |
|
3. Create elements |
Model>Elements>Create Elements... |
|
4. Define general link properties - Linear properties - Nonlinear properties |
Model>Boundaries>General Link Properties... |
|
5. Assign general link |
Model>Boundaries>General Link... |
|
6. Define boundary conditions |
Model>Boundaries>... |
|
7. Enter the static loads |
Load>Self Weight... Load>Assign Floor Loads... |
|
8. Enter masses |
Model>Structure Type... Model>Masses... |
|
9. Enter the time history loads 1) Generate time history load for vertical (gravity) loads - Define Time History Load Case - Define Time Forcing Functions (Normal type) - Enter Time Varying Static Load 2) Generate time history load for seismic loads - Define Time History Load Case - Define Time Forcing Functions (Earthquake record) - Enter the ground acceleration |
Load>Time History Analysis Data> Time History Load Cases... Time Forcing Functions... Time Varying Static Load... Ground Acceleration... |
|
10. Enter Eigenvalue Analysis Control (Ritz Vector) |
Analysis>Eigenvalue Analysis Control... |
|
11. Perform analysis |
Analysis>Perform Analysis... |
|
12. Check analysis results - Displacement / Velocity / Acceleration - Force diagrams - Stresses - Time history graphs of general links - Story Drift |
Results>Time History Results> Disp/Vel/Accel... Force Diagram (Beam/Truss/General Link)... Stress (Beam/Truss)... Time history graph... Results>Result Tables>Story>Story Drift (Time History Analysis) |
Call
From the Main Menu select Model > Boundaries > General Link Properties.
Select Geometry > Boundaries > General Link Properties in the Menu tab of the Tree Menu.
Entry
To enter or add new properties
of general link elements, click the .jpg)
button.
To
modify the properties of general link elements already defined, select
a name from the list of General Link Properties, click the .jpg)
button and change appropriate data entries.
To modify
the properties of general link elements already defined, select a name
from the list of General Link Properties, click the .jpg)
button
and change appropriate data entries.
.bmp)
NameEnter the name for which the properties of nonlinear link elements will be defined.
Application TypeSelect the type of general link element. The types applied to analysis are largely classified into Element Type and Force Type.
Element Type: The Element Type general link element directly reflects the nonlinear behavior of the element by renewing the element stiffness matrix in the process of analysis.
Force Type: The Force Type general link element does not renew the element stiffness matrix. And rather, it reflects the nonlinear behavior indirectly by converting the member force calculated on the basis of the nonlinear properties into an external force.
Property TypeA specific link element is selected for an Application Type. The Element Type general link element provides 3 types; Spring, Linear Dashpot and Spring and Linear Dashpot. The Force Type general link element provides 6 types; Viscoelastic Damper and Hysteretic System used to represent damping devices, Lead Rubber Bearing Isolator and Friction Pendulum System Isolator used to represent base isolators, compression-only Gap element and tension-only Hook element.
Note
Among the Element Type General Link Elements, Spring Type (6 degrees of
freedom : Dx, Dy, Dz, Rx, Ry & Rz) can be reflected in Pushover analysis.
Also linear and inelastic analyses can be performed if the linear and
inelastic hinge properties are assigned to the General Link Element. Inelastic
hinge properties can be defined in Model > Property > Inelastic
Hinge Property.
DescriptionEnter a brief description for the properties.
.jpg)
Self WeightEnter the total weight of the nonlinear link element. The entered self weight is equally divided and distributed to both ends of the element and converted into Static Load or Mass.
Use MassThe user may specify additional mass for the general link element.
Note
Self-weight of a General Link should be entered in Total Weight under Self Weight. Entered Total Weight will be applied to the direction assigned from Load>Self Weight for static analysis, and will be converted into nodal masses for dynamic analysis. In addition, check on Use Mass and input Total Mass to use specific mass separately from the nodal masses converted from Total Weight. However, if 'Do not Covert' is selected from Model>Structure Type> Conversion of Structure Self-weight into Masses, nodal masses converted from Total Weight and Total Mass will not be reflected in the analysis.
Linear PropertiesSpecify whether or not the individual springs of the 6 degrees of freedom of the general link element exist, and enter the corresponding effective stiffness.
Stiffness and Damping are entered for the Element Type, and Effective Stiffness and Effective Damping are entered for the Force Type general link element.
The stiffness or effective stiffness of a general link element is used for linear static and dynamic analyses. If modal superposition and direct integration methods are used in a linear time history analysis, the effective damping applies only when 'Group Damping' is selected for the structure. The Element Type general link element in a nonlinear time history analysis reflects the initial element stiffness based on the entered stiffness.
And if it relates to inelastic hinge properties, the stiffness is renewed in the analysis.
The Force Type general link element, on
the other hand, retains the element stiffness based on the effective stiffness.
Even if nonlinear properties are defined, the stiffness matrix remains
unchanged. Especially, the effective stiffness in a boundary nonlinear
time history analysis using the Force Type general link element represents
imaginary stiffness to avoid rigid action in the algorithm. If the effective
stiffness value is very large in nonlinear analysis, non-convergence may
occur in the process of repetitive analyses, and as such an appropriate
value should be entered. It is common practice to specify the initial
stiffness of damping and isolator devices.
DOF: Check in the box to specify whether or not the springs of the 6 deformation degrees of freedom exist.
Dx, Dy, Dz: Translational deformation degrees of freedom in the x, y & z directions of the Element Coordinate System
Rx, Ry, Rz: Rotational deformation degrees of freedom about the x, y & z axes of the Element Coordinate System
Effective Stiffness
Nonlinear Spring PropertiesCheck in the box to specify nonlinear spring properties for the 6 springs of the nonlinear link element by entering the parameters defining the nonlinear properties.
At this point, those springs that can be
defined with nonlinear properties are limited to the degrees of freedom,
which already have Linear Spring Properties. That is, the limitation applies
to the degrees of freedom for which the DOF check boxes of Linear Spring
Property are already checked in.
DOF: Check in the box to specify whether or not the nonlinear properties of the corresponding degrees of freedom exist.
Nonlinear Properties: Checking in the box prompts the dialog box. Enter the parameters defining the properties of the corresponding nonlinear springs.
Shear Spring LocationCheck in the box to specify the locations of the shear springs.
The locations are defined by the ratios of relative distances from the starting node N1 to the total length. Dy and Dz represent the shear springs in the ECS y and z - axes respectively.
If the locations of the shear springs are specified, the end moments differ due to the shear forces (Difference in moments = shear force x member length). Conversely, if the locations of the shear springs are unspecified, the end moments are always equal without being affected by the shear forces.
Entry
of parameters pertaining to nonlinear properties of individual springs
Enter the parameters defining the nonlinear properties of individual springs for 6 types of nonlinear link elements.
Viscoelastic DamperViscoelastic Damper consists of a linear spring and a (non) linear viscosity damper connected in parallel, which are in turn connected by a spring linking two nodes for each of the 6 degrees of freedom. In addition, MIDAS/Gen provides three types of Viscoelastic Damper models.
Damper Type = Maxwell Model
Maxwell Model consists of a linear spring and a viscosity damper connected in series, as shown in the figure below, and is used for Fluid Viscoelastic Device analysis.
Force-displacement relationship of Maxwell Model is given by
|
|
Damping (Cd): Damping coefficient of viscoelastic damper Reference Velocity (V0): Value to make velocity term dimensionless Note In general, 1.0 will be entered, but it depends on the change in the length units . Damping Exponent (s): Exponent defining the nonlinear viscosity damping property of the viscoelastic damper (Viscosity damping force acts in the opposite direction to the deformation rate and is proportional to the absolute value of the deformation rate to the power of s). Note Viscosity damper can be modeled as either a linear viscosity damper ( s=1), which is proportional to the deformation rate, or a nonlinear viscosity damper (0.0<s<1.0), which is proportional to the deformation rate to the power of s. In general, Damping Exponent is 0.35~1.00. Bracing Stiffness (kb): Stiffness of connecting member (specify the value) |
Damper Type = Kelvin (Voigt) Model
Kelvin Model consists of a linear spring and a viscosity damper connected in parallel, as shown in the figure below, and is used for Solid Viscoelastic Device analysis.
Force-displacement relationship of Kelvin Model is given as below. Since the right side is all known terms, the force acting in viscoelastic damper can be obtained from the equation.
_Model.jpg)
|
|
Damper Stiffness (kd): Stiffness of viscoelastic damper
Damping (Cd): Damping coefficient of viscoelastic damper
Reference Velocity (V0): Value to make velocity term dimensionless Note In general, 1.0 will be entered, but it depends on the change in the length units.
Damping Exponent (s): Exponent defining the nonlinear viscosity damping property of the viscoelastic damper (Viscosity damping force acts in the opposite direction to the deformation rate and is proportional to the absolute value of the deformation rate to the power of s). Note Viscosity damper can be modeled as either a linear viscosity damper (s=1.0), which is proportional to the deformation rate,or a nonlinear viscosity damper(0.0<s<1.0)which is proportional to the deformation rate to the power of s. In general, Damping Exponent is 0.35~1.00. |
Damper Type = Damper Brace Assembly Model
Damper Brace Assembly Model is a Kelvin Model connected by a spring, as shown in the figure below, and is used for analyzing the bracing as a vibration control device.
Force-displacement relationship of Damper Brace Assembly Model is given as below. Since the right side is all known terms, the force acting in viscoelastic damper can be obtained from the equation.
|
|
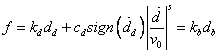
Damper Stiffness (kd): Stiffness of viscoelastic damper Damping (Cd): Damping coefficient of viscoelastic damper Reference Velocity (V0): Value to make velocity term dimensionless Note In general, 1.0 will be entered, but it depends on the change in the length units. Damping Exponent (s): Exponent defining the nonlinear viscosity damping property of the viscoelastic damper (Viscosity damping force acts in the opposite direction to the deformation rate and is proportional to the absolute value of the deformation rate to the power of s). Note Viscosity damper can be modeled as either a linear viscosity damper (s=1.0), which is proportional to the deformation rate, or a nonlinear viscosity damper (0.0<s<1.0), which is proportional to the deformation rate to the power of s. In general, Damping Exponent is 0.35~1.00. Bracing Stiffness (kb): Stiffness of connecting member (specify the value) |
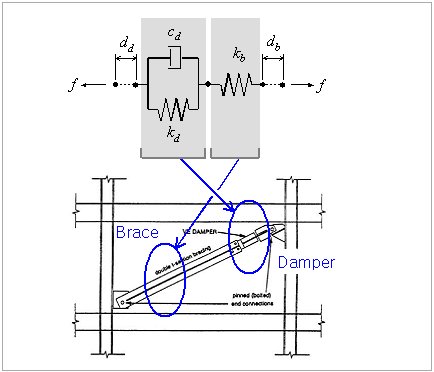
GapGap consists of 6 springs. The deformations of the node N2 relative to the node N1 for all 6 degrees of freedom in the element coordinate system can be represented. If the absolute values of the negative relative deformations become greater than the initial gaps in the springs, the stiffnesses of the corresponding springs will be activated. A linear viscosity damping coefficient can be additionally entered in parallel with each Gap spring.
Stiffness (k): Stiffness of gap spring
Open (o): Initial gap within the Gap spring
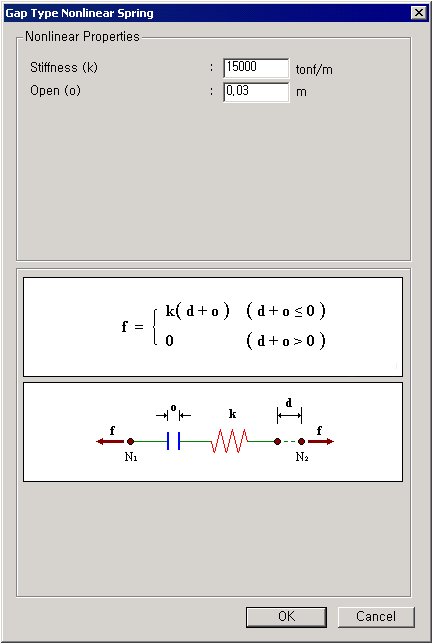
HookHook consists of 6 springs. The deformations of the node N2 relative to the node N1 for all 6 degrees of freedom in the element coordinate system can be represented. If the absolute values of the positive relative deformations become greater than the initial slippage distances in the springs, the stiffnesses of the corresponding springs will be activated. A linear viscosity damping coefficient can be additionally entered in parallel with each Hook spring.
Stiffness (k): Stiffness of hook spring
Open (o): Initial slippage distance within the hook spring
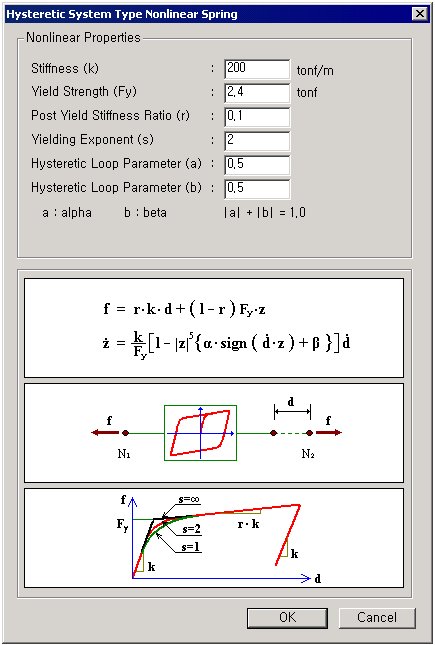
Hysteretic SystemHysteretic system consists of 6 independent springs having the properties of Uniaxial Plasticity. In addition, a linear viscosity damping coefficient can be entered in parallel with each Hysteretic System spring.
Stiffness (k): Initial elastic spring stiffness before yielding
Yield Strength (Fy): Yield strength of spring
Post Yield Stiffness Ratio (r): Ratio of post-yield stiffness to elastic stiffness prior to yielding
Yelding Exponent (s): Parameter determining the shape of Force-Deformation curve near the yield strength transition region (Larger values lead close to the Bi-linear shape.)
Hysteretic Loop Parameter (メ): Parameter determining the shape of hysteretic curve
Hysteretic Loop Parameter (モ): Parameter determining the shape of hysteretic curve
Lead Rubber Bearing
IsolatorLead Rubber Bearing Isolator retains the
properties of coupled Biaxial Plasticity for the 2 shear deformations
and the properties of independent linear elastic springs for the remaining
4 deformations. In addition, a linear viscosity damping coefficient can
be entered in parallel with the spring of each degree of freedom.
The parameters defining the shear deformation springs are as follows:
Stiffness (k): Initial elastic spring stiffness before yielding
Yield Strength (Fy): Yield strength of spring
Post Yield Stiffness Ratio (r): Ratio of post-yield stiffness to elastic stiffness prior to yielding
Hysteretic Loop Parameter (メ): Parameter determining the shape of hysteretic curve
Hysteretic Loop Parameter (モ): Parameter determining the shape of hysteretic curve
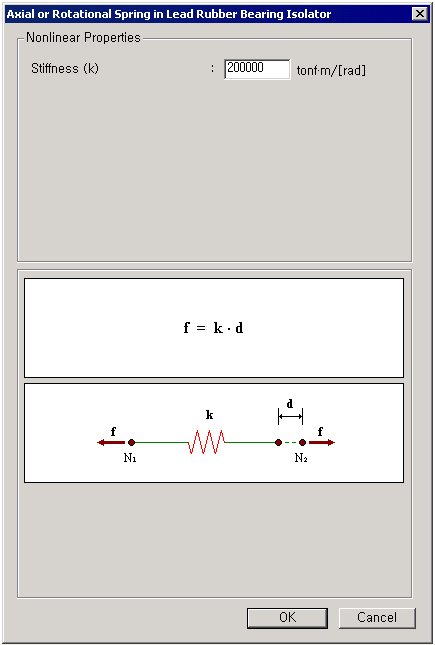
The parameters defining the axial deformation and 3 rotational deformation springs are as follows:
Stiffness (k): Stiffness of spring
Friction Pendulum
System IsolatorFriction Pendulum System Isolator retains
the properties of coupled Biaxial Plasticity for the 2 shear deformations,
the nonlinear property of the Gap behavior for the axial deformation and
the properties of independent linear elastic springs for the remaining
3 rotational deformations. The Force-Deformation relationship of the axial
spring of the friction pendulum system type isolator is identical to that
of Gap with the initial gap of 0. In addition, a linear viscosity damping
coefficient can be entered in parallel with the spring of each degree
of freedom.
The parameters defining the axial deformation spring are as follows:
Stiffness (k): Stiffness of spring
.jpg)
The parameters defining the shear deformation springs are as follows:
Stiffness (k): Initial shear stiffness prior to sliding
Friction Coefficient, Slow (レs): Friction coefficient for slow deformation velocity
Friction Coefficient, Fast (レs): Friction coefficient for fast deformation velocity
Rate Parameter (r): Rate of the change of friction coefficient with respect to the deformation velocity
Radius of Sliding Surface (R): Radius of the sliding surface curvature
Hysteretic Loop Parameter (メ): Parameter determining the shape of hysteretic curve of shear spring
Hysteretic Loop Parameter (モ): Parameter determining the shape of hysteretic curve of shear spring
.jpg)
The parameters defining the 3 rotational deformation springs are as follows:
Stiffness (k): Stiffness of spring
.jpg)
