|
1D
幾何特性として長さを持ち、2個(1次)、または3個(2次)の節点で構成される要素です。3D形状を1D要素で表現するので断面(サイズ、形状)を定義する必要があり、これを利用して2次元要素でモデル化した後、計算されます。
FEA NXでは以下の図のように多様な形状が提供されます。断面特性定義の際にOffset位置が追加設定できます。
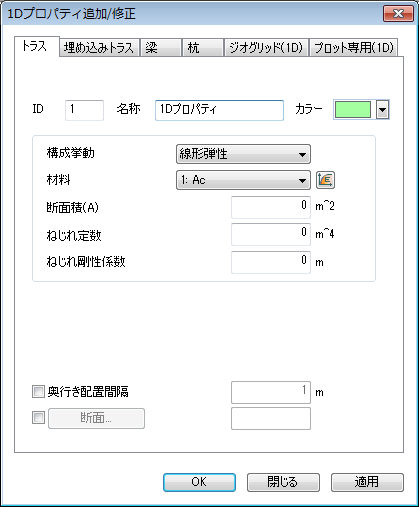
<実際モデル> <有限要素モデル>
|

QUAD-4 6400個
<ソリッド四角形>
|

QUAD-4 3400個
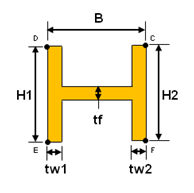
<H-断面>
|

QUAD-4 3400個
<H-断面>
|
<断面自動モデル化>
|
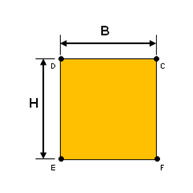
<ソリッド四角形>
|
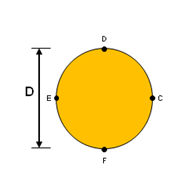
<ソリッド円形>
|
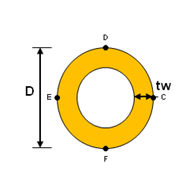
<杭>
|
|
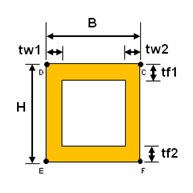
<ボックス断面>
|
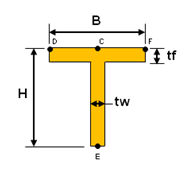
<T-断面>
|
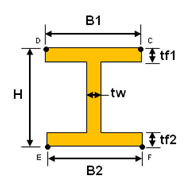
<H-断面>
|
|
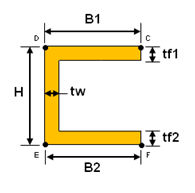
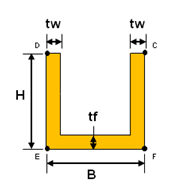
<チャンネル>
|
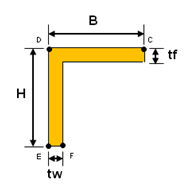
<角>
|
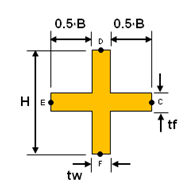
<十字形断面>
|
|
<I-断面>
|
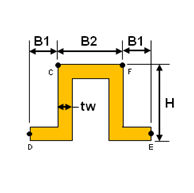
<チャンネル 1>
|
<ハット形断面>
|
<断面形状及び寸法の定義>

2D
幾何特性として面積を持つ三角形(Triangle)、または四角形(Quadrilateral)です。3D形状を2D要素で表現するので厚さを定義する必要があります。厚さは均一厚さ、または位置別変断面が設定できます。
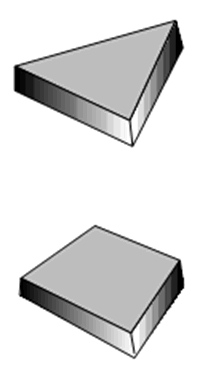 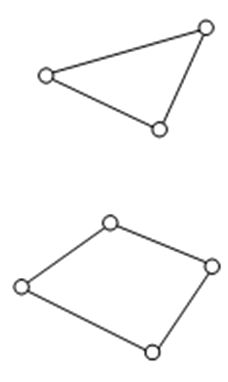
<実際モデル> <有限要素モデル>

3D
幾何特性として体積を持つ四面体(Tetrahedron)、または六面体(Hexahedron、 Brick)形状の要素です。
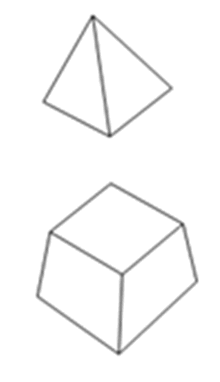 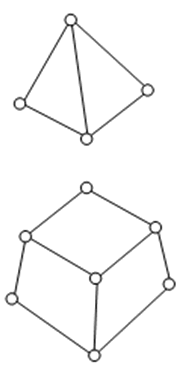
<実際モデル> <有限要素モデル>
断面積(A : cross sectional area)
断面積(cross sectional area)は部材が引張または圧縮力(axial force)を受ける場合、これに抵抗する軸剛性(axial stiffness)を計算したり、部材に発生した応力を計算するに使用され、計算手法はH-断面に対して次の通りです。
FEA NXの内部で断面積を計算する方法は二つあります。一番目の方法は提供される断面形状に対するデータベースから要求される断面の寸法を入力して自動的に断面積を計算する方法であり、二番目の方法としてはユーザーが直接断面積を計算して入力する方法があります。一番目の方法は使用上に便利であるという長所がありますが、実際の断面形状で発生する接合部のボルト、接合穴及びリベット接合穴等による断面積の減少要因は考慮せず、ユーザーが直接計算された断面積を入力する二番目の方法がより正確な結果が表せます。
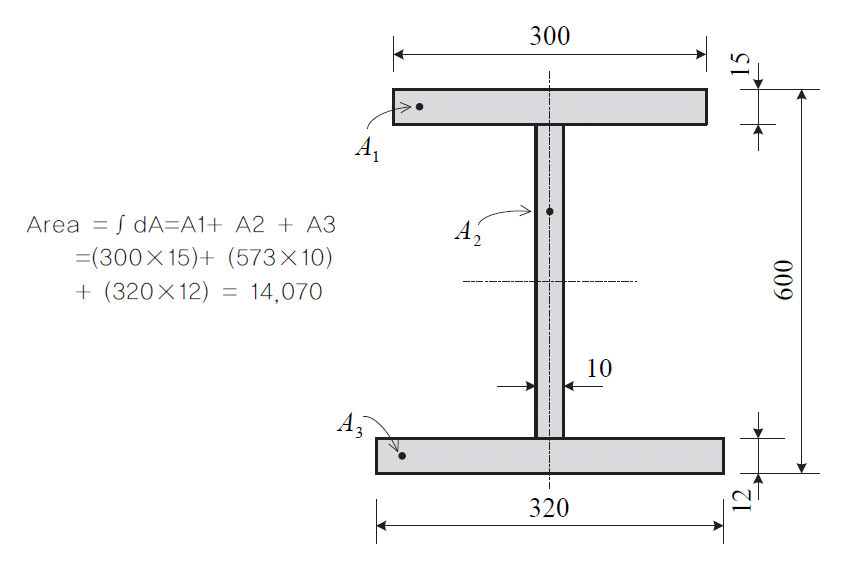
<断面積の計算例>

ねじれ剛性 (Ixx : torsional resistance)
ねじれ剛性はねじれモーメントに抵抗する剛性で次の様に表現されます。
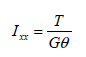
ここで、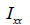 : ねじれ剛性 (torsional resistance), : ねじれ剛性 (torsional resistance),
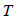 : ねじれモーメント (torsional moment or torque), : ねじれモーメント (torsional moment or torque),
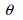 : ねじれ角度(angle of twist) : ねじれ角度(angle of twist)
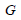 : せん断弾性係数 : せん断弾性係数
ねじれ剛性は上式でのようにねじれに抵抗する剛性であり、ねじれによるせん断応力を決定する極慣性断面二次モーメント(polar moment of inertia)とは違います。
(ただし、円形断面や厚さの厚い円筒断面の場合はねじれモーメントと極慣性断面二次モーメントが一致します。)
ねじれ剛性の場合とSaint-venantのねじり理論を利用して次の様に計算されます。
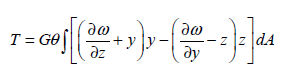
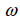 は関数で(warping function) は関数で(warping function) 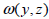 の関数であり、有限要素法で以下の方程式を利用して計算します。 の関数であり、有限要素法で以下の方程式を利用して計算します。
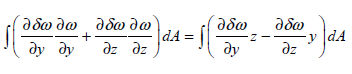
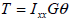 なので、ねじれ剛性成分は次の様に表せます。 なので、ねじれ剛性成分は次の様に表せます。
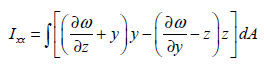

有効せん断面積 (Asy, Asz : effective shear area)
せん断力に対する有効せん断面積(effective shear area)は部材断面の要素座標系y軸、またはz軸方向へ作用するせん断力(shear force)に抵抗する剛性(shear stiffness)の計算に必要です。
もし、有効せん断面積を入力しなかった場合には該当方向のせん断ひずみが無視されます。
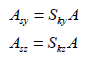
ここで、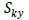 : 要素座標系y軸方向へ作用するせん断力に抵抗する有効せん断係数 : 要素座標系y軸方向へ作用するせん断力に抵抗する有効せん断係数
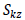 : 要素座標系z軸方向へ作用するせん断力に抵抗する有効せん断係数 : 要素座標系z軸方向へ作用するせん断力に抵抗する有効せん断係数
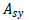 : 要素座標系y軸方向へ作用するせん断力に抵抗する有効せん断面積 : 要素座標系y軸方向へ作用するせん断力に抵抗する有効せん断面積
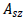 : 要素座標系z軸方向へ作用するせん断力に抵抗する有効せん断面積 : 要素座標系z軸方向へ作用するせん断力に抵抗する有効せん断面積
内部で断面物性を計算したり、データベースから入力される場合には該当せん断剛性成分が自動考慮され、有効せん断係数の計算方法は曲げモーメントで発生されたせん断力による関数(warping function)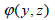 とSaint-venantのねじり理論のねじりによる関数 とSaint-venantのねじり理論のねじりによる関数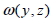 を利用して以下のように計算されます。 を利用して以下のように計算されます。
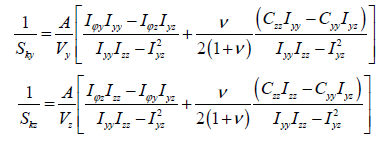
ここで、
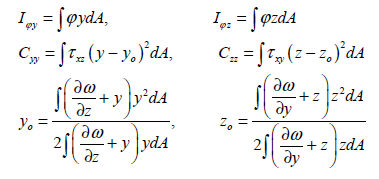

断面二次モーメント (Iyy, Izz : area moment of inertia)
断面二次モーメント(area moment of inertia)は曲げモーメント(bending moment)に抵抗する曲げ剛性(flexural stiffness)を計算するに使用され、該当断面の図心軸で次のような式に従って計算されます。
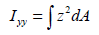
|
Section element
|
b
|
h
|
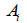
|
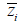
|
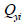
|
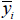
|
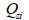
|
|
①
|
10
|
4
|
40
|
2
|
80
|
5
|
200
|
|
②
|
2
|
10
|
20
|
9
|
180
|
5
|
100
|
|
③
|
8
|
3
|
24
|
15.5
|
372
|
5
|
120
|
|
total
|
-
|
-
|
84
|
-
|
632
|
-
|
420
|
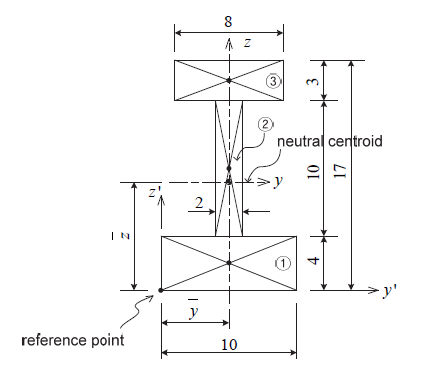
<断面一次モーメント及び図心の計算>
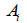 : area : area
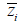 : distance from the reference point to the centroid of the section element in the z′-axis direction : distance from the reference point to the centroid of the section element in the z′-axis direction
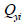 : distance from the reference point to the centroid of the section element in the y′-axis direction : distance from the reference point to the centroid of the section element in the y′-axis direction
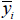 : first moment of area relative to the reference point in the y′-axis direction : first moment of area relative to the reference point in the y′-axis direction
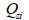 : first moment of area relative to the reference point in the z′-axis direction : first moment of area relative to the reference point in the z′-axis direction
-
中立軸の位置計算 ( 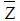 , , 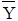 ) )
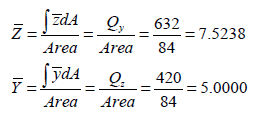
-
断面二次モーメントの計算 ( 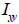 , , 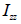 ) )
|
Section element
|
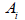
|
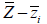
|
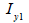
|
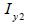
|
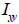
|
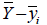
|
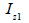
|
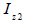
|
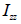
|
|
①
|
40
|
5.5328
|
1224.5
|
53.3
|
1277.8
|
0
|
0
|
333.3
|
333.3
|
|
②
|
20
|
1.4672
|
43.1
|
166.7
|
209.8
|
0
|
0
|
6.7
|
6.7
|
|
③
|
24
|
7.9762
|
1526.9
|
18.0
|
1544.9
|
0
|
0
|
128.0
|
128.0
|
|
total
|
|
2794.5
|
238.0
|
3032.5
|
|
0
|
468.0
|
468.0
|
|
<表. 断面二次モーメントの計算例>
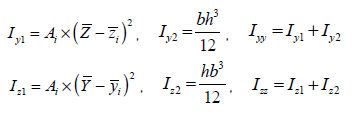

断面相乗モーメント(Iyz : area product moment of inertia)
断面相乗モーメント(area product moment of inertia)は非対象断面の応力成分を計算するに使用され、その定義は次のようになります。
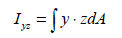
H、 pipe、 box、 channel、 tee形断面の様に要素座標系y、 z軸の中のある1つの軸に対して対象である場合にはIyz=0となり、angle形断面のようにある1つの軸に対しても対象でない場合にはIyz≠ 0なので応力成分の計算時に考慮しなければなりません。
Angle形断面の断面相乗モーメントの計算方法は以下の図の様になります。
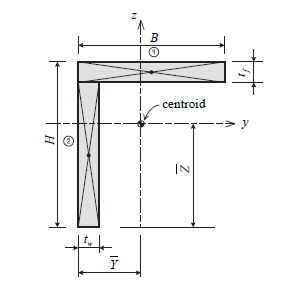 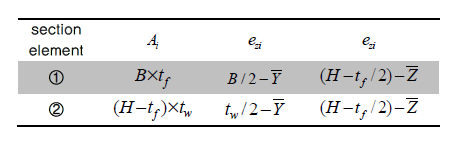
<angle形断面の断面相乗モーメントの計算>
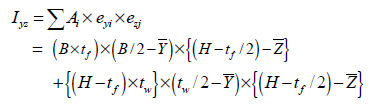
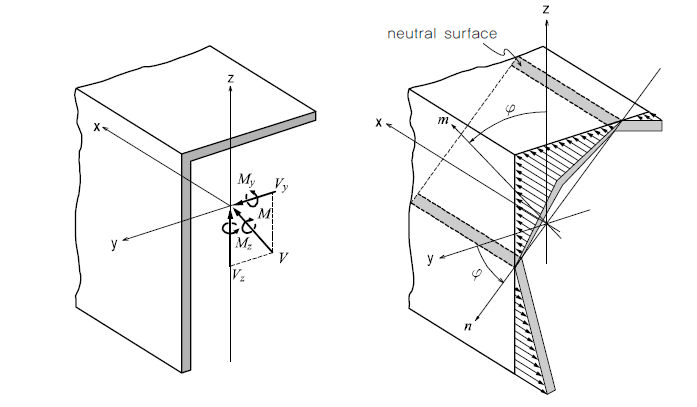
<非対称形断面での曲げ応力分布図>
中立軸(neutral axis)は曲げモーメントによる部材内の曲げ応力が‘0(zero)’になる位置を通る軸をいい、 -軸が中立軸となります。 -軸は -軸に対して垂直を成す軸です。
中立軸では曲げモーメントによる曲げ応力が‘0’なので次の関係式から中立軸の方向が求められます。
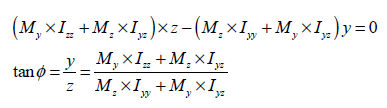
曲げモーメントによる断面の曲げ応力を計算するに適用される一般式は次の通りです。
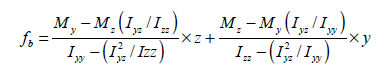
もし、H形断面の場合には 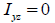 となるので、 となるので、
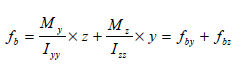
ここで、 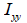 : 要素座標系y軸に対する断面二次モーメント、 : 要素座標系y軸に対する断面二次モーメント、
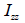 : 要素座標系z軸に対する断面二次モーメント、 : 要素座標系z軸に対する断面二次モーメント、
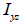 : 断面相乗モーメント、 : 断面相乗モーメント、
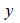 : 要素断面の中立軸から曲げ応力を計算しようとする位置までの要素座標系y軸方向の距離、 : 要素断面の中立軸から曲げ応力を計算しようとする位置までの要素座標系y軸方向の距離、
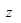 : 要素断面の中立軸から曲げ応力を計算しようとする位置までの要素座標系z軸方向の距離、 : 要素断面の中立軸から曲げ応力を計算しようとする位置までの要素座標系z軸方向の距離、
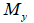 : 要素座標系y軸に対する曲げモーメント、 : 要素座標系y軸に対する曲げモーメント、
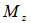 : 要素座標系z軸に対する曲げモーメント : 要素座標系z軸に対する曲げモーメント
要素座標系 y軸及びz軸方向で作用するせん断力に対するせん断応力を計算するに適用される一般式は次の様になります。
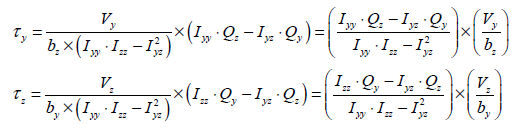
ここで、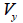 : 要素座標系y軸方向へ作用するせん断力、 : 要素座標系y軸方向へ作用するせん断力、
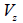 : 要素座標系z軸方向へ作用するせん断力、 : 要素座標系z軸方向へ作用するせん断力、
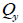 : 要素座標系y軸に対する断面一次モーメント、 : 要素座標系y軸に対する断面一次モーメント、
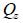 : 要素座標系z軸に対する断面一次モーメント、 : 要素座標系z軸に対する断面一次モーメント、
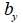 : せん断応力を計算しようとする位置での要素座標系y軸と直角を成す断面の厚さ、 : せん断応力を計算しようとする位置での要素座標系y軸と直角を成す断面の厚さ、
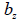 : せん断応力を計算しようとする位置での要素座標系z軸と直角を成す断面の厚さ : せん断応力を計算しようとする位置での要素座標系z軸と直角を成す断面の厚さ

断面一次モーメント(Qy, Qz : first moment of area)
断面一次モーメント(first moment of area)は断面の任意の位置でせん断応力を計算するに使用されて以下のように計算します。
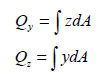
断面がy、 z 両軸の中である一つの軸に対して対称である場合、任意の位置でのせん断応力は次のように計算されます。
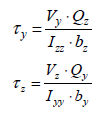
ここで、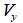 : 要素座標系y軸方向へ作用するせん断力、 : 要素座標系y軸方向へ作用するせん断力、
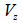 : 要素座標系z軸方向へ作用するせん断力、 : 要素座標系z軸方向へ作用するせん断力、
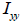 : 要素座標系y軸に対する断面二次モーメント、 : 要素座標系y軸に対する断面二次モーメント、
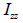 : 要素座標系z軸に対する断面二次モーメント、 : 要素座標系z軸に対する断面二次モーメント、
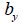 : せん断応力を計算しようとする位置での要素座標系y軸と直角を成す断面の厚さ、 : せん断応力を計算しようとする位置での要素座標系y軸と直角を成す断面の厚さ、
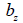 : せん断応力を計算しようとする位置での要素座標系z軸と直角を成す断面の厚さ : せん断応力を計算しようとする位置での要素座標系z軸と直角を成す断面の厚さ
要素厚さ
FEA NXでは平面応力要素、ジオグリッド要素(2D)、シェル要素、平面ひずみ要素、軸対称要素、線形界面要素等を定義する為に要素の厚さを定義しなければなりません。この中で平面ひずみ要素と軸対称要素及び線形界面要素の場合は内部的に単位厚さの1を使用していて使用単位系によって厚さを定義することもできます。
平面応力要素、ジオグリッド要素(2D)、シェル要素の場合はユーザーが直接入力した厚さの値を使用します。この時にシェル要素の場合は回転自由度を持っていて厚さ方向で別度の積分が実行されます。
|


![]()
![]()