応答スペクトル解析法はモード別の時間応答の最大絶対値のスペクトルデータをモード重ね合わせの原理を利用して組合わす解析法です。モード別に最大値が発生する時間の同時性を考慮しないで最大絶対値のみを組合わすので線形時刻歴(モード)解析の近似解とみられます。代わりに、モード別の相関関係を考慮してモード重ね合わせを行い、同時性に対する誤差を補正します。

スペクトルデータ

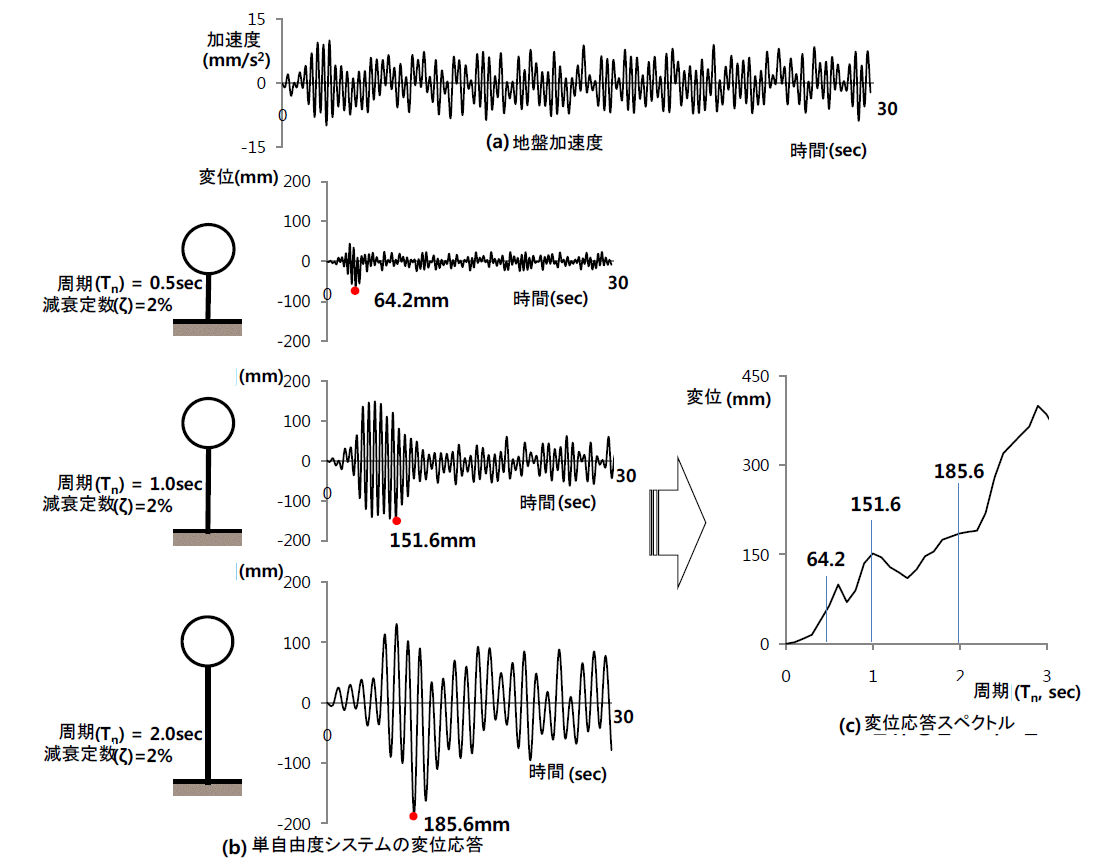
一つの時刻歴を持つデータに対して単自由度システムの減衰比を固定して周期(質量、剛性)を変えつつ求めた変位(或いは速度、加速度)の最大絶対値の組が一つのスペクトルデータとなります。構造物がモード別に減衰比が異なることがあり得るので、一般的に一つの減衰比に対するスペクトルデータで解析するよりは減衰比によっていくつかのスペクトルデータを作成して、減衰比に対して補間する手法を使用します。また、スペクトルデータを作成する際に使用した周期の間隔が構造物の固有周期とは異なることがあるので、固有周期に対しても補間をします。補間方法は線形と対数補間法を共に支援します。また、スペクトルデータは特定の持っているデータを変換して使用するよりは該当地域の歴史地震波を統計して作った設計応答スペクトルを使用するのが一般的です。一般的に一つの減衰比を持つ設計応答スペクトルを使用するので、このような場合には補間でなく補正する方式を適用します。

<単自由度システムの変位応答スペクトル作成>

減衰の考慮

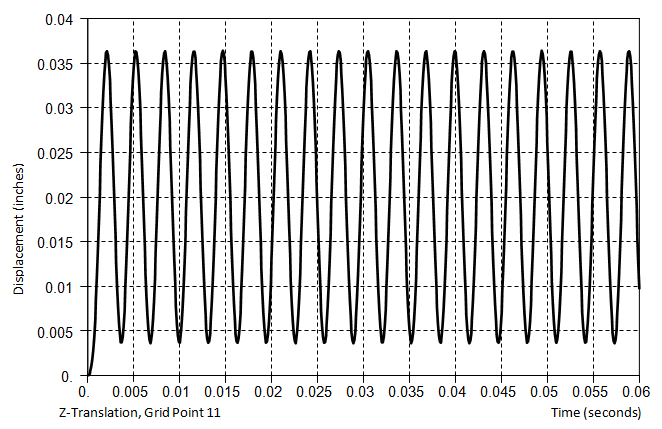
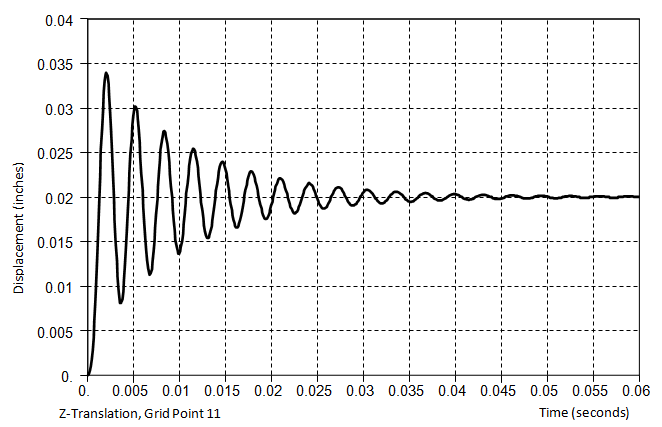
正確な動的解析をする為には減衰の考慮が必須的です。全ての実際構造物は無限に振動することはできなく、分子水準でのエネルギー損失または構成要素間の相互作用による構造物のエネルギー損失の減衰がシステムに適用されて構造物の振動を漸次的に弱化させます。特に、固有振動数付近で構造物が刺激を受ける場合(共振効果)には減衰値が解析結果に支配的な影響を与えるので注意しなければなりません。

             <減衰が無い場合>                                                   <減衰効果がある場合>

対象の構造物の正確な減衰比は実験で決定しなければならなく、一般的に使用される構造物の減衰比は次の表のようになります。

一般的に数値解析上で建物の減衰効果を表現する為にはモード減衰が最も多く使用されます。

モード減衰は振動系の各次数の固有振動数に対して減衰値を決めるもので大きくは比例減衰と非比例減衰で分類できます。比例減衰の質量比例型、剛性比例型、 レーリー(Rayleigh)型の減衰が使用できます。質量比例型減衰は空気抵抗などによる外部粘性減衰を表現したもので減衰行列が質量に比例すると仮定します。一方、剛性比例型減衰は逸散減衰効果(振動エネルギーの地盤への放出効果)が直接表現され難く、減衰剛性に比例すると仮定するので高次モードの減衰を過大評価する恐れがあります。レーリー減衰(Rayleigh damping)はこのような剛性比例型での高次モードの減衰定数を修正したもので質量比例型と剛性比例型の和で表現できます。