メッシュ Valence
メッシュの内部節点が属した要素個数を“Valence”といいますが、Valenceによってメッシュのタイプを構造的メッシュ(Structured Mesh)と非構造的メッシュ(Unstructured Mesh)で区分します。
構造的メッシュ
内部節点のValenceが全て同一なメッシュです。
FEA NXではメッシュ>マップドメッシュメニューで多様な方法で構造的メッシュを作成することができます。
非構造的メッシュ
内部節点のValenceが節点によって異なるメッシュです。
FEA NXではメッシュ>オートメッシュメニューで多様な方法で非構造的メッシュを作成することができます。
下図の2次元四角形メッシュの例を利用してValence(λ)の意味とこれに対する構造的メッシュと非構造的メッシュの差を見てみます。
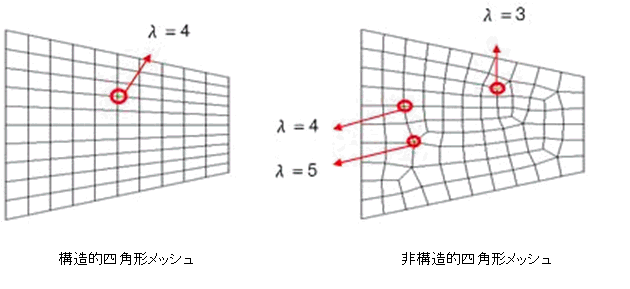
図の構造的四角形メッシュでValenceが4である内部節点は4つの要素に共有されて各要素は360°/4=90°の稜角を持ち、要素の形状が良いです。しかし、非構造的四角形メッシュでは内部節点のValence( λ)によって各要素が360°/λの稜角( λ=3 -> 120° , λ=5 -> 72°)を持ちます。そのために、節点のValenceが4から遠くなるほど該当節点を持つ四角形要素の稜角が90°から遠ざかるので要素形状が悪くなります。2次元の四角形 メッシュではValenceが4の場合が最もよく(構造的メッシュ)、できる限りValenceが3~5間になるようにメッシュを構成する方が望ましいです。
構造的メッシュは形状が良い代わり原則的にいくつかの制約条件が要求されます。2次元の構造的メッシュが作成される過程を見せてくれる次の図からこのような 要求条件を見てみます。
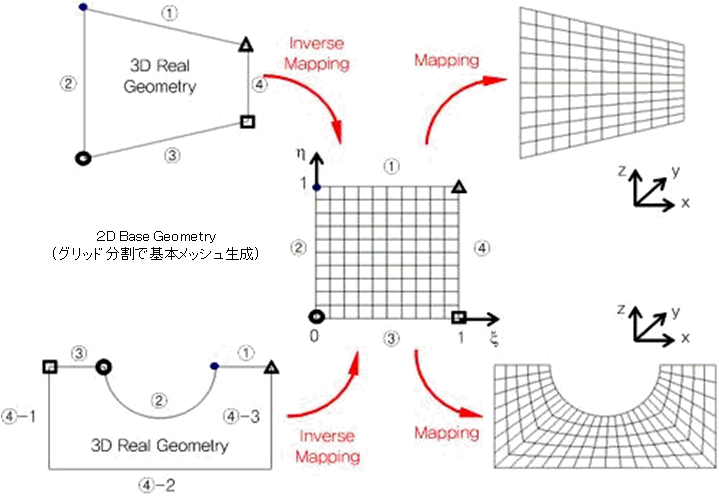
<構造的メッシュの作成過程>
図から分かるように構造的メッシュのは2Dの正方形のベース幾何で格子分割で基本メッシュを作成した次に、このメッシュを3Dの実際幾何でMappingする手法によって作成されます。
このような作成方法の特徴から構造的メッシュのは次の2つの要求条件が満足される幾何にのみ作成されます。
正方形のベース幾何を構成するために4つの基準稜点が明確に定義できる必要があります。
FEA NXでは凸多角形の場合にプログラムが自動に4つの稜点を探して必要な場合にはユーザが手動で4つの稜点を指定することもできます。4つの稜点が定義できな い幾何は手動で適切に分割した後に各分割領域に対してメッシュを作成しなければなりません。
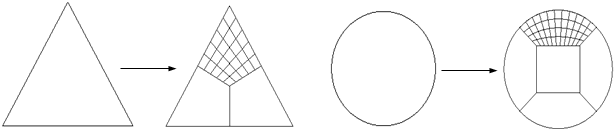
単なる格子分割で基準メッシュを作成するので2Dベース幾何上で向かい合う対エッジまたは対エッジグループ(①-③, ②-④)間の要素分割個数が一致しなければ なりません。
構造的メッシュを作成するために手動でメッシュサイズを指定する場合に要素の大きさより分割個数で指定する方が望ましいです。
構造的メッシュを作成とは違って非構造的メッシュを作成の作成は対象幾何の形状、構成及び分割個数などにどんな制約条件も要求しないので複雑な任意 形状に対しても簡単かつ便利にメッシュを作成することができます。
FEA NXは3つの非構造的メッシュ作成方法を提供します。
Loop Mesher
Looping アルゴリズムを利用して対象領域に直接四角形メッシュを作成するメッシュ作成方法です。
Loop Mesherは対象領域の境界を正確に表現でき、対象領域の回転に無関係に常に同一な形状のメッシュを作成し、特に1:2が超える要素大きさに対しても滑らかに 遷移される四角形メッシュを作成するという長所があります。しかし、アルゴリズムの特性上対象モデルの形状によって作成されるメッシュの直交性(Orthogonality)と 規則性(Regularity)が多少落ちる場合もあり、領域の内部に任意の点と線が含まれる場合に該当内部点/線周りの要素形状が他の領域に比べて相対的によくないかも しれません。たとえば、完全に四角形のみで構成されたメッシュ(Full Quad Mesh)を作るためには全ての境界が偶数個で分割されなければなりませんがそうでない場合 には一部三角形要素が含まれます。Loopingアルゴリズムは単純連結(Simply-connected)領域だけに適用可能です。
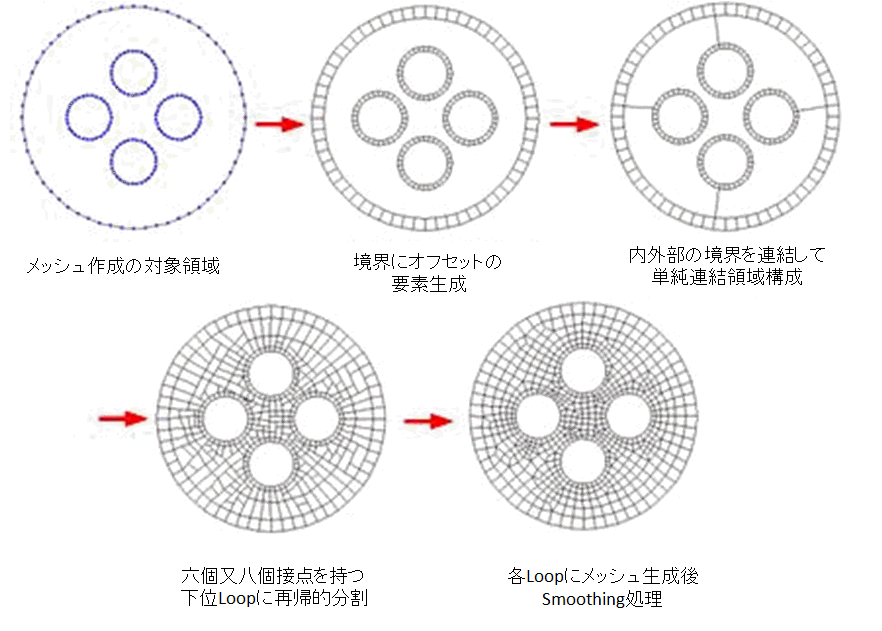
<Loop Mesherの メッシュ生成方法>
Grid Mesher
Grid Mesherは基準格子を用いて対象領域内部に四角形要素を作成し、領域内部の四角形メッシュと領域の境界間に節点連結法で四角形または三角形要素を作成します。
Grid Mesherは直交性/規則性が最も優れたメッシュが作成できるという長所があります。しかし、基準格子を利用するアルゴリズムの特性上1:2を超える要素サイズに対してはメッシュ遷移処理が滑らかでないという短所があります。そして、基本的にメッシュ作成過程で領域内部の点と線が共に考慮されるので該当の内部点/線の周
りに形状の良い要素が作成されます。
Grid Mesherは四角形と三角形がともに作成される混合メッシュと三角形メッシュが作成でき、適用されるメッシュの大きさが同一な場合に最も形状が良いメッシュを作成します。
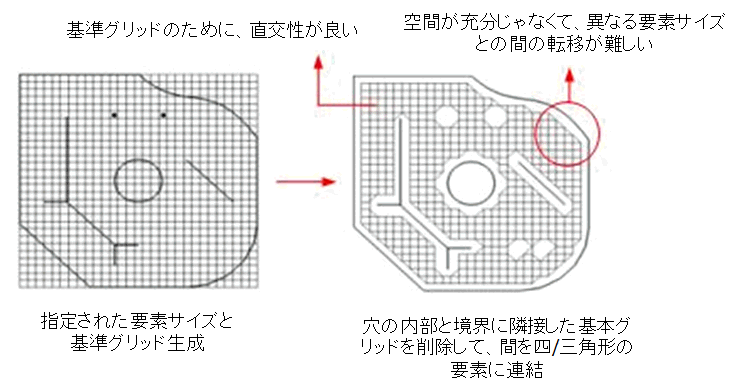
<Grid Mesherが基準グリッドを利用してメッシュを生成する方法>
Delaunay Mesher
代表的なメッシュ作成方法であるDelaunayアルゴリズムを利用したメッシュ作成方法です。三角形メッシュ作成に優れた性能をお見せし、特に内部の点と線が存在 する場合にもこれを基準で自由に要素サイズが指定できます。
正しい要素タイプの選択と要素の形状は解析結果に大きな影響を与えます。そのため、正しい解析結果を得るためには解析対象の構造的特性と望む解析結果を基に 適合した要素の種類を選択しなければならなく、メッシュを作成した後には要素の連結関係と要素の形状を確認しなければなりません。
次は要素の選択とメッシュの作成時に参考できる基本的な事項です。
要素の大きさが小さく、要素形状が正多角形と正多面体に近いほどよい解析結果が得られます。(Compact and Regular)
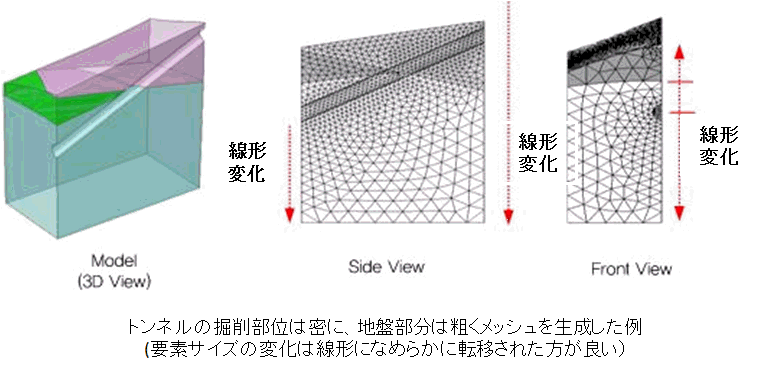
要素の個数と解析時間は反比例するので効率的な解析を実行するためには事前に適切なメッシュ密度分布を計画した後、メッシュを作成する方が望まれます。 (a) 重要解析部位、 (b) 幾何形状の変化の激しいところ、 (c) 材質または特性の変わる場所、 (d) 荷重の変わる場所、 (e) 結果の変化が激しいと予想され場所 では粗密な(Fine)メッシュを作成したほうが望ましいです。逆に重要でない部位と結果の変化が殆どないと予想される場所にはメッシュを荒く(Coarse)作成して 全体要素個数を調節するようにします。
三角形要素(2D)と四面体要素(3D)は四角形要素(2D)と六面体要素(3D)に比べると相対的に強(Stiff)く挙動します。そのため、三角形、四面体要素よりは四角形 や六面体要素を使用することが望ましいです。同様に1次要素も2次要素に比べて相対的に強く挙動するので1次要素よりは2次要素を使用する方が良いです。 特に、三角形及び四面体要素はできる限り2次要素を使用するようにします。
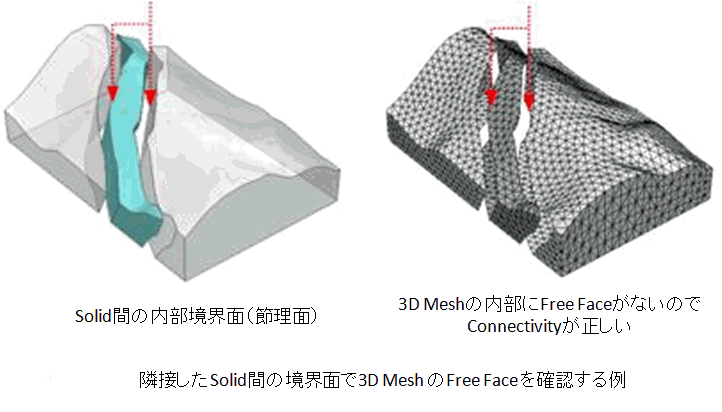
メッシュを作成した次には必ず要素の連結関係(Connectivity)を確認するようにします。2D Meshではフリーエッジ、3D Meshではフリーフェースが存在するか どうかを確認します。
プログラムが提供する多様な要素形状チェック機能を利用して要素形状の適合性を確認します。特に、幾何形状の変化に比べてメッシュがあまりにも荒く作成 された部位では形状の良くない要素が作成される可能性が相対的に高いので注意が必要です。少なくとも2D Meshでは凸でない四角形要素(Non-convex Quadrilateral: Jacobian Ratio ≤ 0)が発生するかどうか、3D Meshでは平面に近い四面体要素(Collapsed Tetra)が発生するかどうかを確認するようにします。