メッシュ作成(Mesh Generation)

要素を構成する節点で定義できる幾何形状(次元)によって要素のタイプを次のように分類することができます。次の分類は節点から形成される幾何形状による分類で、要素の構造的な挙動による分類とは異なります。構造的挙動による分類(例: トラス、棒)とそれぞれの特徴はAnalysis Manualを参考します。

スカラー(Scalar)要素

1つまたは2つの節点で構成されて特別な幾何特性を持たない要素です。Mass, Damper, Spring 要素などがこれに該当します。

1D 要素 (Line)

幾何特性で“長さ”を持ち、2つ(1次)または3つ(2次)の節点で構成される要素です。トラス、棒要素などがこれに該当します。

2D 要素 (Plane)

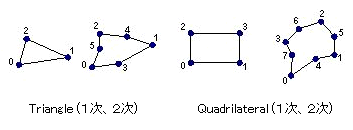
幾何特性で“面積”を持つ三角形(Triangle)または四角形(Quadrilateral)要素です。平面応力、平面ひずみ、軸対象、板要素などがこれに該当します。特に板(Plate)要素は3次元シェル(Shell)構造物のモデル化に最も多く使用される非常に重要な要素で、オプション指定によって多様な挙動を自由に描写できます。

角にのみ節点を持つ1次要素(低次要素)と角や各辺の中央にも節点を持つ2次要素（高次要素）があります。

3D 要素 (Solid)

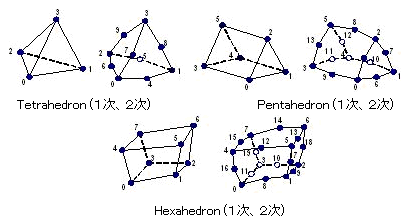
幾何特性で“堆積”を持つ四面体(Tetrahedron)、五面体(Pentahedron, Wedge, Triangular Prism)、六面体(Hexahedron, Brick)要素です。

3次元ソリッドのモデル化に使用され、角にのみ節点を持つ1次要素(低次要素)と角及び各辺の中央にも節点を持つ2次要素(高次要素)があります。

その他

以上の要素分類に該当されない要素です。剛体挙動を表現する剛体(Rigid)要素と荷重と質量を従属節点で配分させる補間(Interpolation)要素などがこれに該当します。

全ての実際構造物は堆積を持つ3次元構造物であり、解析では要素に対象構造物の材質と体積などを与えてその挙動を表現します。そのため、要素は① 節点で定義される幾何形状と ② 材質(Material)、そして ③ 体積計算などのために追加的に必要な特性(Property)によって定義されます。

上のような幾何形状による要素分類で1D, 2D, 3D要素定義に必要な最も基本的な共通の特性(Property)は下の表のようになります。

一般的なメッシュ作成作業は対象幾何の次元、メッシュのタイプに無関係に共通的に下図のようなプロセスで構成されます。

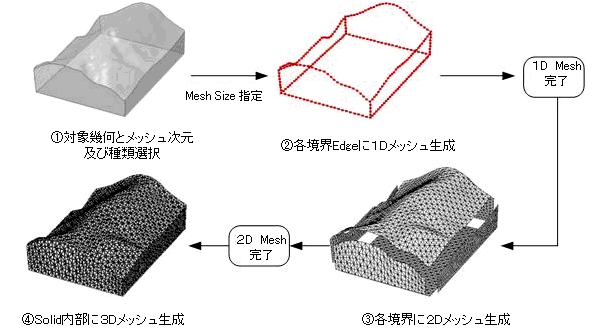
1D メッシュ、 2D メッシュ、 3D メッシュに対してそれぞれのメッシュ作成プロセスを整理すると次のようになります。

1D メッシュ (1D Mesh)

選択したエッジを指定されたメッシュサイズを基準に分割してメッシュを作成します。

2D メッシュ (2D Mesh)

1D メッシュ作成プロセスを辿った後(必要時に内部的にプログラムが自動実行)、作成された境界1D メッシュを基にユーザが指定した2D メッシュ作成アルゴリズムまたはプログラムが自動に選択したアルゴリズムを利用して対象フェースにメッシュを作成します。



3D メッシュ (3D Mesh)

1D メッシュと2D メッシュの作成プロセスを辿った後(必要な段階は内部的にプログラムが自動実行)、作成された境界2D メッシュを基に対象ソリッドの内部にメッシュを作成します。

メッシュ作成時の注意事項

• 正常的な2Dメッシュを作成するためには対象フェースの境界エッジに作成された1Dメッシュが正常的に完全に閉じていなければなりません。同じように3Dメッシュが正常的に作成されるためにはソリッドの各境界フェースに作成された2Dメッシュが完全に閉じていなければなりません。ここで正常的に閉じていなければなられい という意味は途切れた区間と互いに交差する区間があってはならないという意味です。

• ユーザの便宜のためにプログラムが多様な幾何個体(ソリッド、フェース、エッジなど)に対するメッシュサイズ指定機能を提供したが、究極的にメッシュ密度を決定 するのはエッジに対するメッシュサイズです。そのため、メッシュ密度が重要なところにはエッジに対するメッシュサイズを指定することが最も確実です。

• 必要な場合にはユーザが低次元のメッシュの作成を手動で処理した後に高次元のメッシュ作成プログラムによって処理することもできます。

<例> 境界2Dメッシュを直接作った次にこれを利用してすぐに3Dメッシュを作成することもできます。つまり、原則的に3Dメッシュを作成するためには境界2Dメッシュが 必要であって、ソリッド（幾何）が必ず要求されるのではありません。