|
地盤の応力-ひずみ挙動は破壊条件に近接するほど非線形になりますが、非線形弾性モデルは地盤係数を変化することでこのような地盤の挙動を描写するモデルです。地盤係数を計算するためにDuncan and Chang (1970)によって提示された数式を使用し、この式で応力-ひずみ曲線は双曲線で地盤係数は拘束応力(confining stress)とせん断応力の関数です。この非線形弾性の材料モデルは三軸圧縮試験や文献から簡単に得られる物性値のみ必要とするため、非常に有用に使用することができます。Duncan and Changの非線形応力-ひずみ曲線はせん断応力 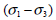 地盤の応力-ひずみ挙動は破壊条件に近接するほど非線形になりますが、非線形弾性モデルは地盤係数を変化することでこのような地盤の挙動を描写するモデルです。地盤係数を計算するためにDuncan and Chang (1970)によって提示された数式を使用し、この式で応力-ひずみ曲線は双曲線で地盤係数は拘束応力(confining stress)とせん断応力の関数です。この非線形弾性の材料モデルは三軸圧縮試験や文献から簡単に得られる物性値のみ必要とするため、非常に有用に使用することができます。Duncan and Changの非線形応力-ひずみ曲線はせん断応力 地盤の応力-ひずみ挙動は破壊条件に近接するほど非線形になりますが、非線形弾性モデルは地盤係数を変化することでこのような地盤の挙動を描写するモデルです。地盤係数を計算するためにDuncan and Chang (1970)によって提示された数式を使用し、この式で応力-ひずみ曲線は双曲線で地盤係数は拘束応力(confining stress)とせん断応力の関数です。この非線形弾性の材料モデルは三軸圧縮試験や文献から簡単に得られる物性値のみ必要とするため、非常に有用に使用することができます。Duncan and Changの非線形応力-ひずみ曲線はせん断応力 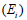 、接線係数 、接線係数 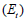 、除荷-再載荷(unloading-reloading)係数 、除荷-再載荷(unloading-reloading)係数 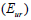 )で定義されます。 )で定義されます。
双曲線モデルの主要非線形パラメータは以下の通りです。
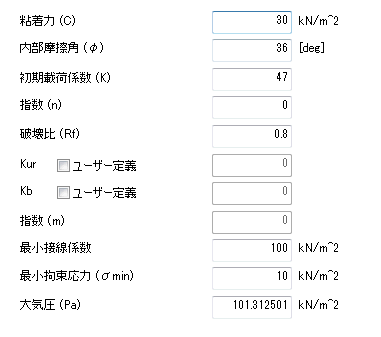
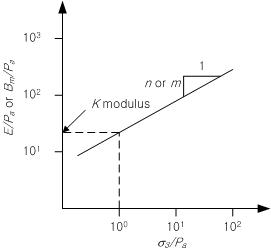
三軸圧縮試験の結果から下の図のように縦軸が 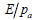 または または 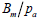 になるようにして横軸を になるようにして横軸を 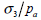 になるようにグラフが描けます。各軸をlogスケールに合わせた後、 になるようにグラフが描けます。各軸をlogスケールに合わせた後、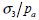 =1 の点での縦軸の値が初期載荷係数(K)となります。縦軸が =1 の点での縦軸の値が初期載荷係数(K)となります。縦軸が 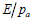 の時、グラフの傾きから指数(n)が求められて の時、グラフの傾きから指数(n)が求められて 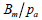 の時のグラフの傾きから指数(m)を求められます。ここで、体積係数 Bm は下式のように定義され、ポアソン比との関係からも予測できます。ここで、ポアソン比は0から0.5以下の値で制限されます。 の時のグラフの傾きから指数(m)を求められます。ここで、体積係数 Bm は下式のように定義され、ポアソン比との関係からも予測できます。ここで、ポアソン比は0から0.5以下の値で制限されます。
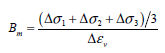
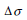 : 主応力の変化量、 : 主応力の変化量、
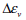 : 体積ひずみの変化量 : 体積ひずみの変化量
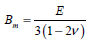
<材料物性の決定>

Duncan and Changの非線形応力-ひずみ曲線は応力状態と応力経路によって三つの地盤係数(初期係数 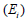 、接線係数 、接線係数 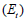 、除荷-再載荷(unloading-reloading)係数 、除荷-再載荷(unloading-reloading)係数 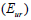 )で定義されます。 )で定義されます。
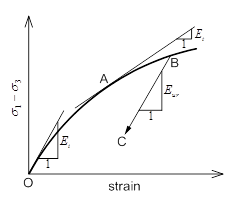
<非線形応力-ひずみ挙動>
ここで、初期係数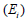 と接線係数 と接線係数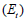 の関係で破壊比(Rf)が求められます。破壊比は双曲線に対する漸近線と最大せん断強度の比で一般的に0.75~1の間の値を持ちます。接線係数 の関係で破壊比(Rf)が求められます。破壊比は双曲線に対する漸近線と最大せん断強度の比で一般的に0.75~1の間の値を持ちます。接線係数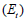 は値があまりにも小さい場合には収束問題を導けるので最小接線係数のデフォルト値は大気圧(Pa)です。 は値があまりにも小さい場合には収束問題を導けるので最小接線係数のデフォルト値は大気圧(Pa)です。
体積係数番号(Kb)は体積係数(Bm)と指数(m)から計算されます。
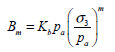
ここで、
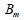 : 体積係数(bulk modulus)、 : 体積係数(bulk modulus)、
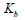 : 体積係数番号、 : 体積係数番号、
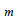 : 指数 : 指数
除荷-再載荷係数番号 は除荷は除荷-載除荷係数 は除荷は除荷-載除荷係数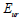 から計算されます。 から計算されます。
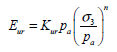
初期係数を求める際に適用される拘束応力は'0(zero)'か負数(引張状態)になる場合、初期係数が'0(zero)'か負数になり得ますので拘束応力に対するか下限値設定が必要であり、設定された最小拘束圧力は0.01Paです。
砂質土の密度によるパラメータの提案値は以下の通りです。(Duncan, J. M. and Chan, C. Y. (1970))
|
Relative density
|
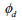
|
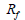
|
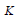
|
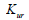
|
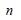
|
|
100% (dense)
|
36.5
|
0.91
|
2000
|
2120
|
0.54
|
|
38% (loose)
|
30.4
|
0.90
|
295
|
1090
|
0.65
|
|
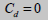 for dense and loose sand for dense and loose sand
|
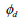 , ,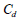 : 乾燥状態での摩擦角と粘着力 : 乾燥状態での摩擦角と粘着力
<表. Summary of stress-strain parameters for uniform fine silica sand>
|
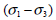 地盤の応力-ひずみ挙動は破壊条件に近接するほど非線形になりますが、非線形弾性モデルは地盤係数を変化することでこのような地盤の挙動を描写するモデルです。地盤係数を計算するためにDuncan and Chang (1970)によって提示された数式を使用し、この式で応力-ひずみ曲線は双曲線で地盤係数は拘束応力(confining stress)とせん断応力の関数です。この非線形弾性の材料モデルは三軸圧縮試験や文献から簡単に得られる物性値のみ必要とするため、非常に有用に使用することができます。Duncan and Changの非線形応力-ひずみ曲線はせん断応力
地盤の応力-ひずみ挙動は破壊条件に近接するほど非線形になりますが、非線形弾性モデルは地盤係数を変化することでこのような地盤の挙動を描写するモデルです。地盤係数を計算するためにDuncan and Chang (1970)によって提示された数式を使用し、この式で応力-ひずみ曲線は双曲線で地盤係数は拘束応力(confining stress)とせん断応力の関数です。この非線形弾性の材料モデルは三軸圧縮試験や文献から簡単に得られる物性値のみ必要とするため、非常に有用に使用することができます。Duncan and Changの非線形応力-ひずみ曲線はせん断応力 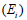 、接線係数
、接線係数 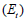 、除荷-再載荷(unloading-reloading)係数
、除荷-再載荷(unloading-reloading)係数 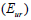 )で定義されます。
)で定義されます。
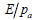 または
または 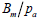 になるようにして横軸を
になるようにして横軸を 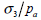 になるようにグラフが描けます。各軸をlogスケールに合わせた後、
になるようにグラフが描けます。各軸をlogスケールに合わせた後、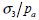 =1 の点での縦軸の値が初期載荷係数(K)となります。縦軸が
=1 の点での縦軸の値が初期載荷係数(K)となります。縦軸が 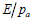 の時、グラフの傾きから指数(n)が求められて
の時、グラフの傾きから指数(n)が求められて 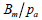 の時のグラフの傾きから指数(m)を求められます。ここで、体積係数 Bm
の時のグラフの傾きから指数(m)を求められます。ここで、体積係数 Bm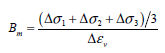
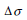 : 主応力の変化量、
: 主応力の変化量、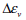 : 体積ひずみの変化量
: 体積ひずみの変化量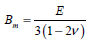

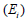 、接線係数
、接線係数 
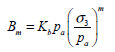
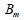 : 体積係数(bulk modulus)、
: 体積係数(bulk modulus)、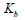 : 体積係数番号、
: 体積係数番号、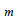 : 指数
: 指数 は除荷は除荷-載除荷係数
は除荷は除荷-載除荷係数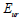 から計算されます。
から計算されます。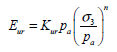
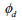
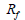
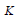
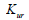
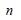
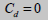 for dense and loose sand
for dense and loose sand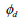 ,
,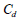 : 乾燥状態での摩擦角と粘着力
: 乾燥状態での摩擦角と粘着力