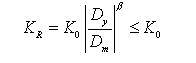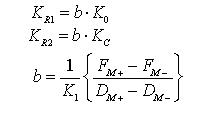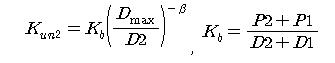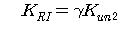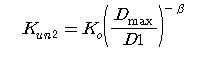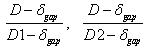Inelastic Hinge Properties
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Add, modify or delete inelastic hinge properties.
Inelastic hinges are applied to inelastic time history analysis only.
The Spring Type hinge defined in General Link Properties can be used for pushover analysis if the inelastic hinge properties are assigned to the hinge. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
From the Main Menu Select Model > Properties > Inelastic Hinge Properties.
Select Geometry > Properties > Inelastic Hinge Properties in the Menu tab of the Tree Menu. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
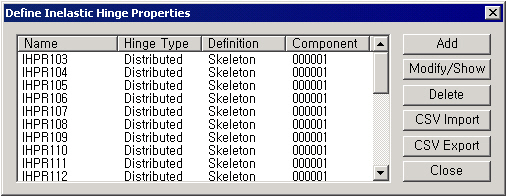
Define Inelastic Hinge Properties dialog box
Click to add Inelastic Hinge Properties.
To modify previously defined Inelastic Hinge Properties, select a property name, click the button and change the input.
To delete previously defined
Inelastic Hinge Properties, select a property name and click the
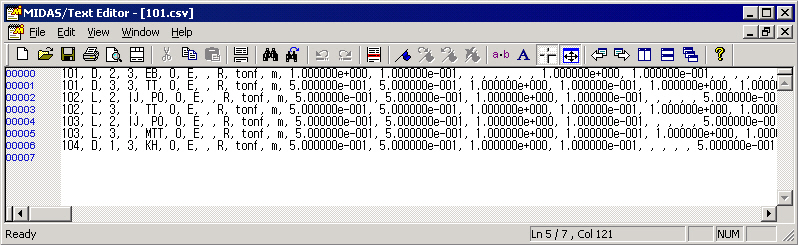
: Import inelastic hinge properties saved in a CSV file.
: Export inelastic hinge properties to a CSV file. Only the inelastic hinge properties defined as User Type will be available for output. Only the inelastic hinge properties defined as Yield Strength (Surface) Calculation Method-User Type and Interaction Type-None will be available for output.
: Close Inelastic Hinge Property dialog box.
CSV Export
Rows 12 ~ 29 are differently entered depending on the Input Type of Yield Properties.
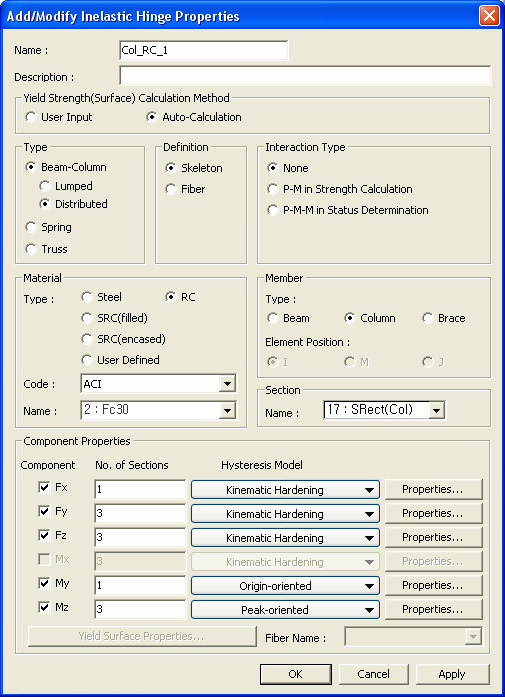
Add/ Modify Inelastic Hinge Properties dialog box
Name
Enter the name representing the inelastic hinge properties.
Description
Enter a brief description for inelastic hinge properties being defined.
Yield Strength (Surface) Calculation Method
User Input: User directly defines inelastic hinge properties.
Auto-calculation: Inelastic hinge properties are automatically calculated using the selected material, section, and member information.
Type
Define the hinge type (Lumped, Distributed, and Spring)
Beam-Column
Lumped: it concentrates the inelastic behavior represented by rotational and translational springs at each end and the center. And the remaining parts are assumed to behave elastically. Inelastic hysteresis behaviors are defined by skeleton curves, which are empirical hysteresis models. The axial component is represented by a spring at the center and two translational components are represented by springs at each end defined by force-displacement relationships. The two flexural components, My and Mz, are represented by springs defined by the relationship between moment and angle of rotation at either I or J or at both ends.
Distributed: Unlike lumped hinges, it assumes inelastic behavior throughout the member. The plastic hinge locations in the length direction of a member assigned by the user are defined as the integration points. The flexibility matrix of a section, which represents the distribution of internal forces, is calculated through the integration points. The number of integration points can be 1 and between 3 and 20. If the number of integration points is 2, the moment at the free end of a cantilever beam does not come to exactly zero due to the inherited characteristic of the integration method. Therefore, two integration points are not permitted. Inelastic hysteresis behavior can be defined by 2 models, empirical Skeleton and Fiber. The hinge behaviors can be expressed by force - deformation relationships in each axis direction, and the hinge hysteresis behavior of the flexural components can be expressed by the relationships of moment and angle of rotation. Inelastic behaviors can be defined for 3 axis components and 2 flexural (My & Mz) components.
Spring
Unlike Lumped and Distributed hinges, which are influenced by the inelastic properties of materials and members, the inelastic plastic hinge properties for the corresponding linear properties of each component of Property Type defined in General Link Properties are defined. The elastic stiffness of each component is defined by effective stiffness and acts as the initial stiffness in inelastic analysis. The inelastic hysteresis behavior of a spring is defined by a skeleton model. The inelastic properties of a spring can be defined for all 3 translational and 3 rotational directions. LRB and HDR type vibration isolator hysteresis models can be defined only by using Spring Type.
Note
Truss
The axial component is represented by a spring at the center defined by the force-displacement relationship. The inelastic hysteresis behavior of a spring is defined by a skeleton model.
Definition
Define the hysteresis behavior model of an inelastic hinge.
Skeleton: It is an empirical hysteresis model, which assumes that the property of each directional component is independent of one another. Each component is defined as a uni-axial hinge hysteresis model. Such independently acting hinges are 3 translational and 3 rotational hinges.
Note
Fiber: Fiber model is used to define multi-axis hinge hysteresis model. In the fiber model, a beam section is divided into fibers, which undergo axial deformations only. By using the fiber model, the user can trace a more accurate moment-curvature relationship compared to using a hysteresis model of the member. The moment-curvature relationship is based on the stress-strain relationship of the fiber material and an assumed strain distribution on the section. Moreover, this model considers translation of neutral axis due to axial force.
Interaction Type
For Column or Brace members, the type of considering interaction between axial force and moment is selected.
None: Interaction between axial force and moments is not considered.
Note
P-M in Strength Calculation: N-M interaction in time history analysis is reflected by calculating the flexural yield strength of a hinge considering the effect of axial force. In this method, the interaction between biaxial bending moments is ignored. The axial force is assumed to act with each directional bending moment independently when the hinge status is evaluated at each time step. Recalculation of bending moment yield strength reflecting axial force is carried out in a loading condition, which satisfies the following three conditions:
1) It must be the first among the sequential time history load cases, which will be consecutively analyzed.
2) Inelastic static analysis must be carried out.
3) Displacement control must be used.
The elements are inelastic beam elements assigned with hinge properties to which P-M interaction is applied. The initial axial and bending moment at this time are determined by the combination of linear elastic analysis results of all the static loads contained in Time Varying Static Load. The factors used in the combination are defined by the Scale Factors specified in Time Varying Static Load.
P-M-M in Status Determination: This method uses a multi-axis hinge hysteresis model in inelastic time history analysis. Interaction between axial force and biaxial moments is realized by applying the plasticity theory. The interaction is considered at each time step through evaluating the status of inelastic hinges using the 3-dimensional yield surface. MIDAS/Civil supports the kinematic hardening type
Note
Material
Type
Select a material type for the inelastic hinge properties to be applied. 5 types are provided - Steel, Reinforced Concrete, Steel Reinforced Concrete composite section (filled), Steel Reinforced Concrete composite section (encased) and User Defined. Depending on the type of selected material, the method of defining the yield stress of each element is evaluated differently.
Steel: The 1st yielding is defined if the maximum flexural stress of a section reaches the yield stress. The 2nd yielding is defined if the flexural stress of the entire section reaches the yield stress.
RC: The first yielding is defined if the maximum flexural stress of a section reaches the cracking stress of concrete. The second yielding is defined if the stress block of concrete reaches the ultimate strength or the rebars yield.
SRC (filled): Concrete filled steel ?same as the steel section calculation codes
SRC (encased): Concrete encased steel ?same as the concrete section calculation codes
User Defined: Properties are calculated using the material properties defined by the user.
Code
A design code is selected, which is used for obtaining yield strength and cracking strength coefficient of concrete for RC and SRC (encased) types only. ACI and AIJ are provided. Cracking strength coefficient used in ACI is 7.5 in lb-in unit, and in AIJ it is 1.8 in kgf-cm unit.
Name
Select a Material Name for which the inelastic hinge will be applied.
Member
Type
Select a member type for which the inelastic hinge will be applied from Beam, Column and Brace.
Element Position
Select a position of the Member Type for applying the inelastic hinge. I, M and J represent i-end, middle (center) and j-end respectively, which are selected only for the RC Beam member type. This is intended to extract reinforcing data from the selected position of RC Beam members.
Section
Name
Select a section name for which the inelastic hinge will be applied.
Component PropertiesInelastic hinge properties by each component of section strength are entered.
Component
Select the components of sectional strength for which properties will be entered. The Spring Type permits properties in all directional components, whereas Lumped and Distributed types permit all but the Mx component.
Hinge Location
Select the locations of lumped inelastic hinges. Axial component is fixed to the center of a member. I-end, j-end or both ends can be selected for the bending moment components.
Num. of Sections
Enter the number of integration points for inelastic hinges of the distributed type. Up to 20 sections are permitted, and moment -curvature relationships are calculated at all the sections corresponding to the points.
Hysteresis Model
Select a hysteresis model for an inelastic hinge.
Properties
Enter the properties of inelastic hinges for each component.
Fiber Name
If a distributed hinge of the fiber type is selected, select a fiber element name.
Yield Surface Properties
If "P-M in Strength Calculation" or "P-M-M in Status Determination" is selected in Interaction Type, enter the related data for P-M interaction curve and 3-D yield surface.
Hysteresis Model
Kinematic hardening type hysteresis model
Kinematic Hardening hysteresis model
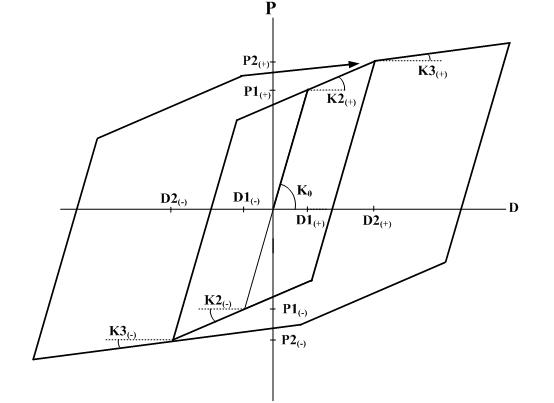
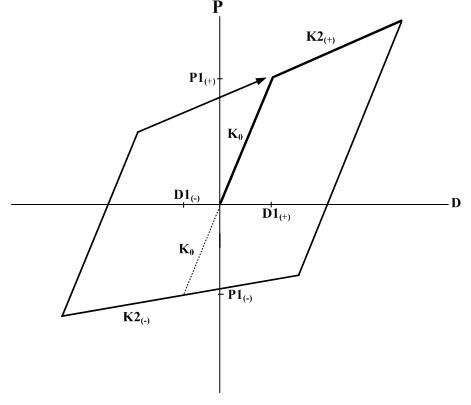
Response points at the initial loading move along a trilinear skeleton curve. The unloading stiffness is identical to the elastic stiffness. It shows the tendency of strength increase with the increase in loading. This is used to model the Bauschinger effect of metallic materials. Accordingly, it is cautioned that energy dissipation may be overestimated for concrete. Due to the characteristic of the model, only the positive (+) and negative (-) symmetry is permitted for the strength reduction ratios after yielding. Origin-oriented type hysteresis model
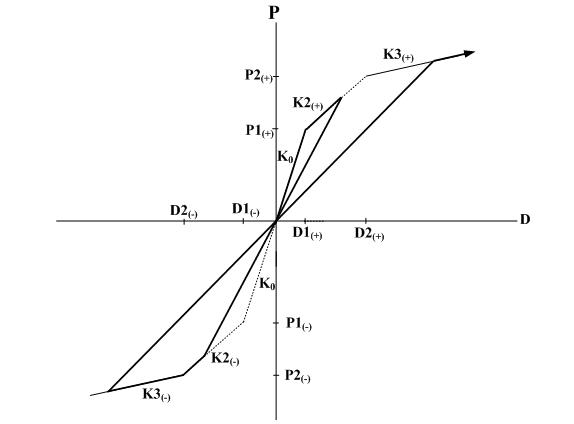
Response points at the initial loading move along a trilinear skeleton curve. Response points at unloading move toward the origin and again move along the skeleton curve after reaching the opposite skeleton curve. Peak-oriented type hysteresis model
Response points at the initial loading move along a trilinear skeleton curve. Response points at unloading move toward the point of maximum displacement on the opposite side. If the first yielding has not occurred on the opposite side, the response points move toward the first yielding point on the skeleton curve.
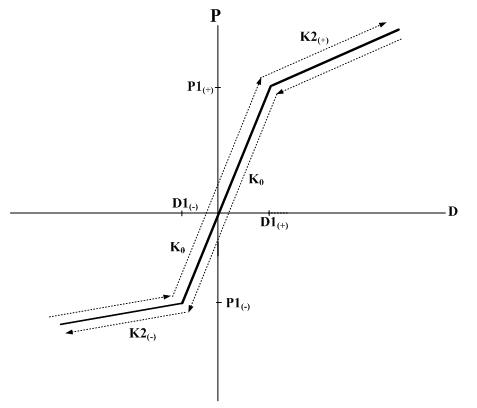
Response points at the initial loading move along a bilinear skeleton curve. Unloading stiffness is obtained from the elastic stiffness reduced by the equation below. As the deformation progresses after yielding, unloading stiffness reduces gradually.
where,
If the sign of loading changes in the process of unloading, response points move toward the point of maximum displacement in the zone of progressing direction. If yielding has not occurred in this zone, the response points move toward the yield point on the skeleton curve. If unloading becomes loading without changing the loading sign, the response points move along the unloading path. If the loading continually increases, loading continues on the skeleton curve again.
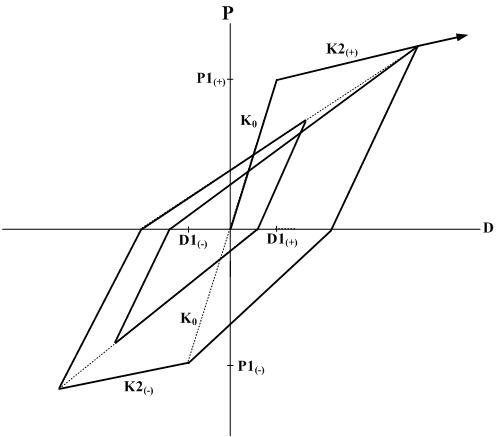
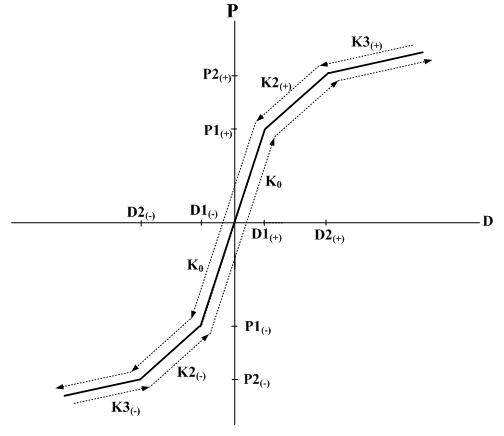
Degrading Trilinear type hysteresis model
Response points at the initial loading move along a trilinear skeleton curve. The load-displacement coordinates at unloading move to the path of reaching the maximum deformation point on the opposite side due to the change of unloading stiffness once in the middle. If yielding has not occurred on the opposite side, the first yielding point is assumed to be the maximum deformation point. The first and second unloading stiffness is determined by the equations below. As the maximum deformation increases, unloading stiffness gradually decreases.
where,
KR1: first unloading stiffness
KR2: second unloading stiffness
K0: elastic stiffness
KC: first yield stiffness in the zone where the loading point is oriented due to unloading
K1: the slope between the origin and the second yield point in the zone where the loading point is oriented due to unloading
b: stiffness reduction ratio. If unloading occurs between the first and second yield points on the skeleton curve, it is fixed to 1.0.
FM+ , FM-: maximum load at each positive (+) and negative (? sides
DM+ , DM-: maximum deformation at each positive (+) and negative (? sides
Response points at the initial loading move along a trilinear skeleton curve. The unloading stiffness is determined by the location of the unloading point on the skeleton curve and whether or not the first yielding has occurred in the opposite side zone.
If unloading occurs between the first and second yield points on the skeleton curve, load-deformation coordinates progress toward the first yield point on the skeleton curve on the opposite side. If the loading sign changes in the process, the coordinates progress toward the maximum deformation point on the skeleton curve in the zone of the progressing direction. If yielding has not occurred in this zone, the coordinates progress toward the first yield point. If the skeleton curve is encountered in the process of progressing, the coordinates progress along the skeleton curve. If unloading takes place in the zone beyond the second yield point on the skeleton curve, the load-deformation coordinates progress following the next unloading stiffness.
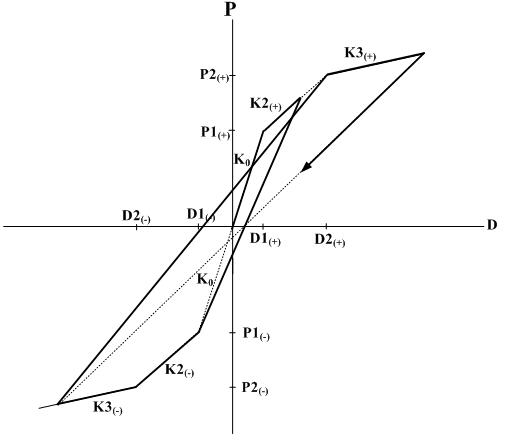
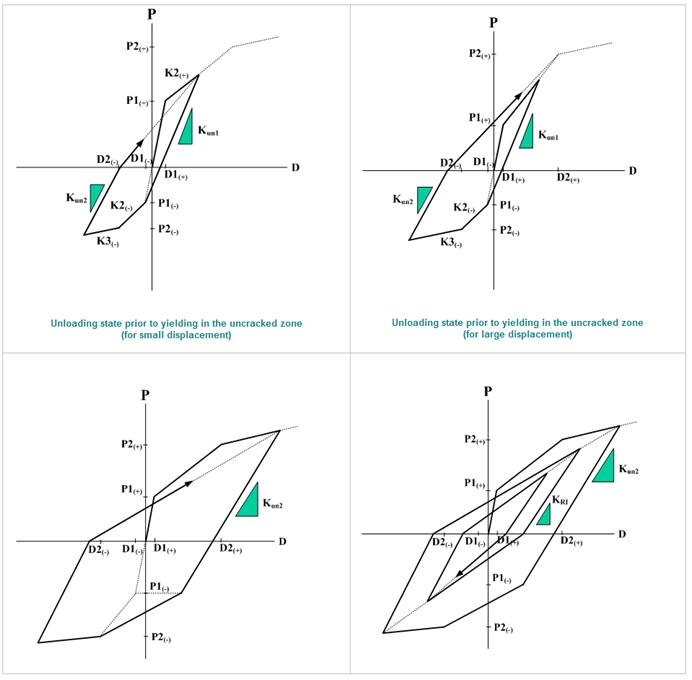
Original Takeda type hysteresis model
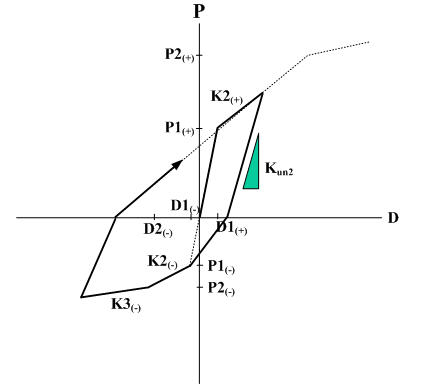
1. The point moves along the trilinear skeleton curve.
2. If unloading occurs from the straight line toward the opposite direction, the point moves toward the first yield point on the opposite side.
3. If the maximum displacement on the opposite side is in the elastic zone, the range of this elastic zone extends to the first yield point on the opposite side.
4. If the maximum deformation on the opposite side exceeds D1, the displacement in this elastic zone is defined up to the point of restoring force becoming 0. If it passes beyond the 0 point, it moves toward the maximum deformation point on the opposite side. The stiffness at unloading from the straight line directed toward this maximum deformation uses the stiffness of unloading from the maximum deformation point on the opposite side.
1. The point moves along the trilinear skeleton curve.
2. If unloading occurs from this straight line toward the opposite direction, the point moves from the unloading point along the straight line of the stiffness obtained from the equation below.
where,
Kun2: unloading stiffness of the outer loop
P1: first yield loading in the zone opposite to the unloading point
P2: second yield loading in the zone to which the unloading point belongs
D1: first yield displacement in the zone opposite to the unloading point
D2: second yield displacement in the zone to which the unloading point belongs
Dmax: maximum deformation in the zone to which the unloading point belongs
β: constant for determining unloading stiffness of the outer loop
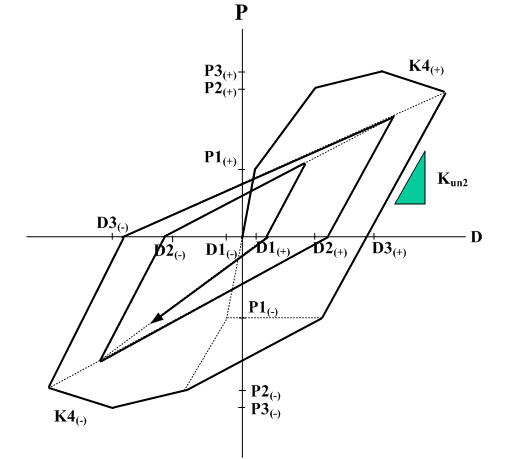
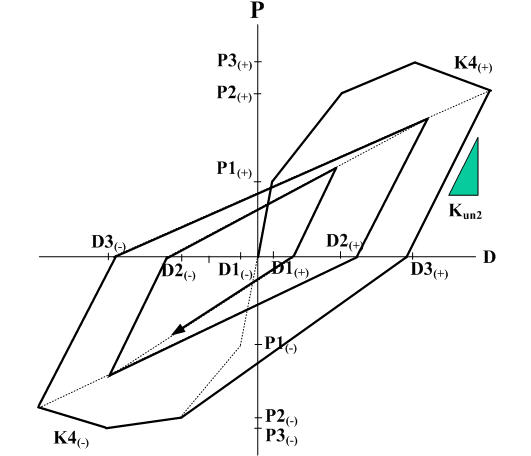
3. If the maximum deformation point on the opposite side does not exceed D1, the range of the slope Kun2 extends up to P1 on the opposite side. If it goes beyond this P1, it directs toward the D2 point. If unloading occurs from the straight line directed toward the D2 point, it moves along the straight line of the slope Kb. If the restoring force exceeds 0, it directs toward the maximum deformation point. If unloading occurs from the straight line directed toward the maximum deformation point, it moves along the slope Kun2. If the restoring force goes beyond 0, it directs toward the maximum deformation point on the opposite side.
4. If the loading sign changes in the process of unloading and while reloading takes place, unloading may occur before reaching the target point on the skeleton curve. Loops are formed in the process, which are all referred to as inner loops. The unloading stiffness within the inner loops is determined by the equation below.
where, KRI: unloading stiffness of inner loop
Kun2: unloading stiffness of outer loop in the zone to which the start point of unloading belongs
γ: reduction factor for unloading stiffness of inner loop
5. If the maximum deformation on the opposite side exceeds D1, the range of the slope Kun2 extends up to the point of restoring force becoming 0, and if it goes beyond 0, it directs toward the maximum deformation point. If unloading takes place from the straight line directed toward this maximum deformation point, D at this point becomes the maximum deformation point of the inner loop. And it moves along the slope Kun2 and directs toward the maximum deformation point if the restoring force exceed the 0 point. Even in the case where unloading takes place from the straight line directed toward this maximum deformation point, D becomes the maximum deformation point of the inner loop and moves along Kun2. If the restoring force goes beyond the 0 point, it directs toward the maximum deformation point.
Takeda Tetra Linear type hysteresis model
Takeda Tetra Linear hysteresis model
The Takeda tetralinear hysteresis model can be applied to beam element and General Link of Spring Type of Lum ped Type and Distributed Type. Modified Takeda type hysteresis model
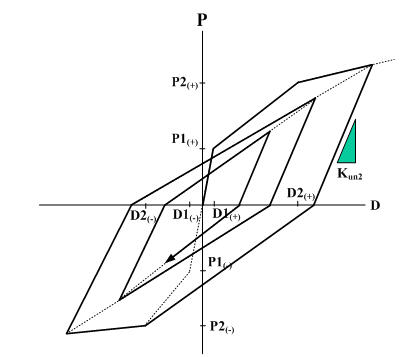
Response points at the initial loading move along a trilinear skeleton curve.
where,
Kun2: unloading stiffness of outer loop
K0: elastic stiffness
D1: first yield displacement in the zone of unloading point
Dmax: maximum deformation in the zone to which the unloading point belongs
β: constant for determining unloading stiffness of the outer loop
The Modified Takeda type hysteresis model can be applied to beam element and General Link of Spring Type of Lumped Type and Distributed Type. Modified Takeda Tetra Linear type hysteresis model
Modified Takeda Tetra Linear Type hysteresis model
The Modified Takeda Tetralinear type hysteresis model can be applied to beam element and General Link of Spring Type of Lumped Type and Distributed Type. Normal Bilinear type hysteresis model
Normal Bilinear Type hysteresis model
Response points at the initial loading move along a bilinear skeleton curve. The unloading stiffness is identical to the elastic stiffness. The Normal Bilinear type hysteresis model can be applied to beam element and General Link of Spring Type of Lumped Type and Distributed Type. Elastic Bilinear type hysteresis model
Elastic Bilinear Type hysteresis model
Regardless of loading and unloading, response points always move along a bilinear skeleton curve without any pattern of curved loops. The Elastic Bilinear type hysteresis model can be applied to beam element and General Link of Spring Type of Lumped Type and Distributed Type. Elastic Trilinear type hysteresis model
Elastic Trilinear Type hysteresis model
Regardless of loading and unloading, response points always move along a trilinear skeleton curve without any pattern of curved loops. The Elastic Trilinear Type hysteresis model can be applied to beam element and General Link of Spring Type of Lumped Type and Distributed Type. Elastic Tetralinear type hysteresis model
Elastic Tetralinear Type hysteresis model
Regardless of loading and unloading, response points always move along a tetralinear skeleton curve without any pattern of curved loops. The Elastic Tetralinear Type hysteresis model can be applied to beam element and General Link of Spring Type of Lumped Type and Distributed Type. LRB Isolator Bilinear type hysteresis model
LRB Isolator Bilinear Type hysteresis model
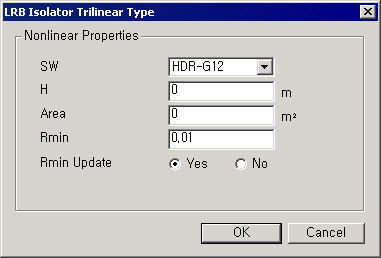
The initial stiffness is calculated by the strain used specifically for calculating the initial stiffness. Movement on a bilinear skeleton curve is the hysteresis rule provided that the strain does not exceed Rmin.
Qd50: yield property
Kp50: yield strength
H: layer thickness
ALF: yield stiffness ratio (1/6.5)
Rmin: strain used specifically for calculating initial stiffness
KE50: initial spring coefficient(spring coefficient at 50% deformation of the LRB device)
LRB Isolator Bilinear type hysteresis model can be applied to General Link of Spring Type only. LRB Isolator Trilinear type hysteresis model
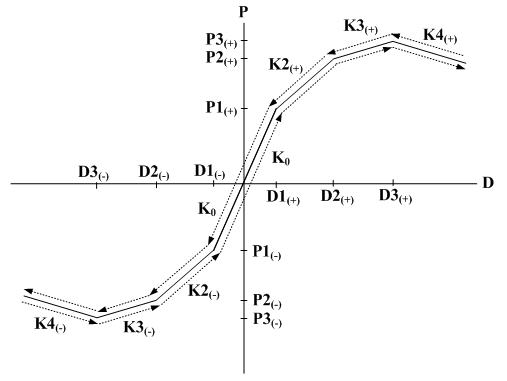
LRB Isolator Trilinear Type hysteresis model
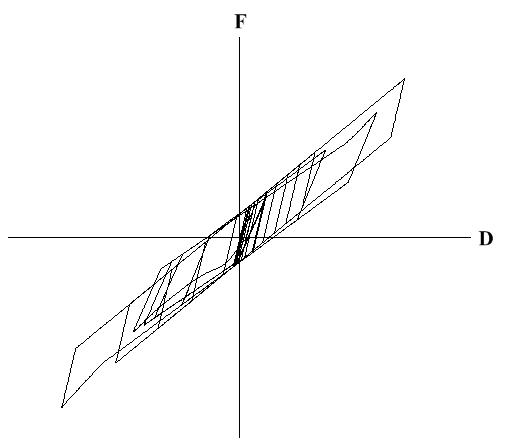
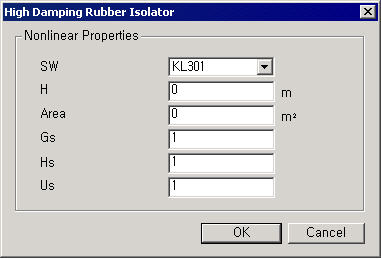
High Damping Rubber Isolator type hysteresis model
High Damping Rubber Isolator Type hysteresis model
Slip Bilinear Type hysteresis model
Slip Trilinear Type hysteresis model
Note
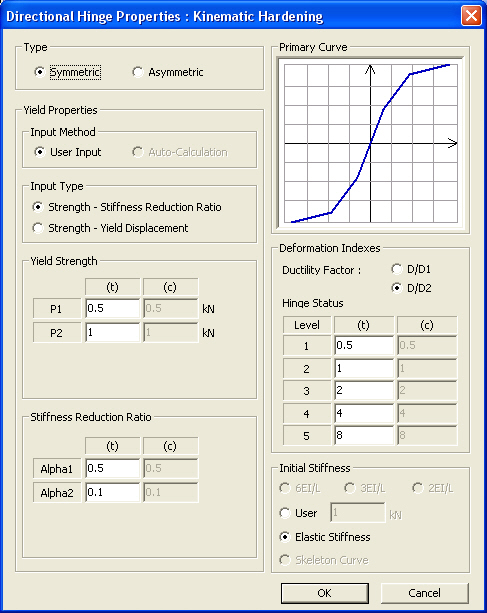
Directional Hinge Properties dialog box
Type
Select whether or not the skeleton curve is symmetrical. Non-symmetry of the curve can be applied to Yield Strength, Stiffness Reduction Ratio and Hinge Status. However, Kinematic Hardening Model does not permit non-symmetry of Stiffness Reduction Ratio due to its characteristics.
Yield Properties
Input Method
User Input: User defines the Yield Properties.
Auto Calculation: The Yield Properties are automatically calculated.
Input Type
Strength-Stiffness Reduction Ratio: Yield Properties are defined by specifying Strength-Stiffness Reduction Ratio.
Strength-Yield Displacement: Yield Properties are defined by specifying Strength-Yield Displacement.
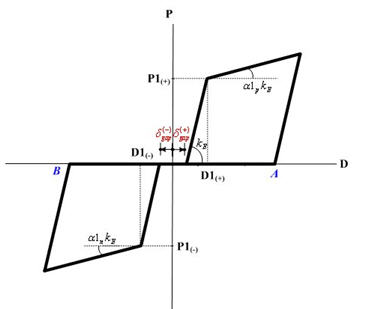
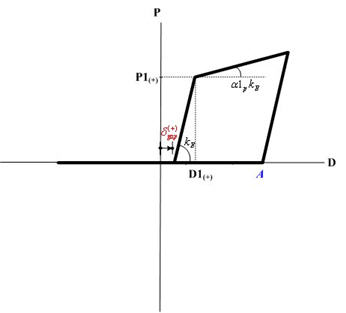
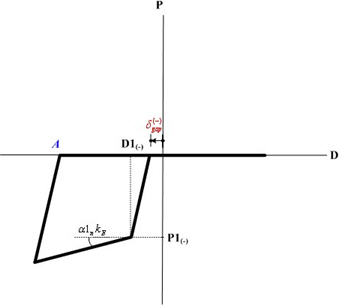
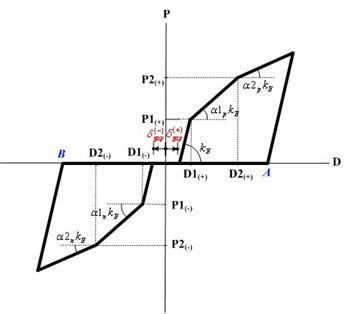
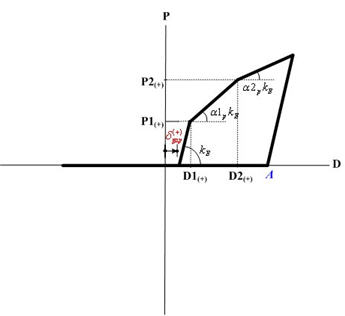
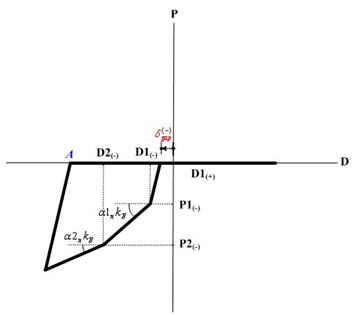
Yield Strength
Yield strength is specified. It is user defined based on material and section properties. The user specifies positive (+) values regardless of tension (t) or compression (c). The program treats compression as negative (-) internally.
P1: P1 represents the first yield strength. If the Material Type is Steel or SRC (filled), the first yield represents the state in which the maximum bending stress of the section reaches the yield stress. If the Material Type is RC or SRC (encased), the first yield represents the state in which the maximum bending stress of the section reaches the cracking stress of concrete. P2: P2 represents the second yield strength. If the Material Type is Steel or SRC (filled), the second yield represents the state in which the bending stress of the entire section reaches the yield stress. If the Material Type is RC or SRC (encased), the second yield represents the state in which the stress in the concrete section reaches the ultimate strength or the stress in reinforcing steel reaches the yield strength. In case of bending, the concrete stress is based on a rectangular stress block. P3: P3 represents the third yield strength.
Stiffness Reduction Ratio
Enter the stiffness reduction ratios of a sloped skeleton curve when Strength - Stiffness Reduction Ratio is selected for Input Type.
α1: Ratio of stiffness immediately after the first yielding divided by the initial stiffness
α2: Ratio of stiffness immediately after the second yielding divided by the initial stiffness, which is defined when the skeleton curve is of Trilinear or Tetralinear type.
α3: Ratio of stiffness immediately after the third yielding divided by the initial stiffness, which is defined when the skeleton curve is of Tetralinear type.
Yield Displacement
Enter the yield displacement of a sloped skeleton curve when Strength - Yield Displacement is selected for Input Type.
D1: first yield displacement component or deformation
D2: second yield displacement component or deformation, which is defined when the skeleton curve is of Trilinear or Tetralinear type.
D3: third yield displacement component or deformation, which is defined when the skeleton curve is of Tetralinear type.
Deformation Indexes
Data required for calculating the indexes, which represent the level of deformation of an inelastic hinge
Ductility Factor: Select a basis of calculating ductility. Depending on the selection by the user, ductility factor is calculated by dividing the current deformation by the first yield deformation or the second yield deformation
Hinge Status: Enter the reference ductility, which classifies the state of a hinge in 5 different levels. In case of a non-symmetric hinge, the hinge status level at each time step is determined by the larger of the positive (+) and negative (-) levels. Level-1 (0.5) signifies the elastic status and Level-2 (1) signifies the yield status. Level-3 (2), Level-4 (4) and Level-5 (8) represent the level of ductility of each member. In analysis results, the status is presented in blue, green, yellowish light green, orange and red colors.
Initial Stiffness
The initial stiffness used in inelastic analysis is either selected or entered by the user.
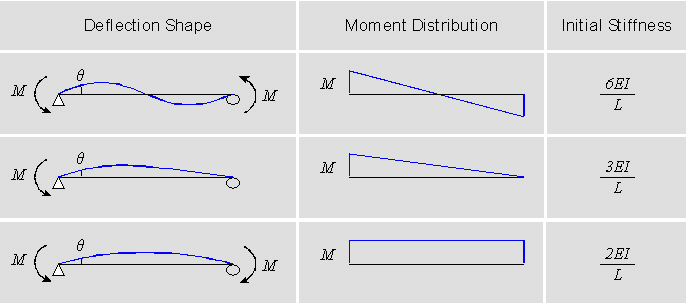
The selection of initial stiffness is founded on the premises of the longitudinal distribution of bending moment. If the bending moments, which are assumed to be linearly distributed, are the same in magnitude with opposite signs at both ends, select 6EI/L. If one end is 0, select 3EI/L. If the magnitudes and the signs are identical, select 2EI/L.
6EI/L , 3EI/L, 2EI/L: Provided that the inelastic hinge is of a lumped type for the bending moment component, the initial stiffness is selected on the basis of the longitudinal distribution of bending moment. This cannot be selected in case of Distributed Type and Spring Type.
6EI/L: when end values of linearly distributed bending moment are identical in magnitude but in opposite directions
3EI/L: when one end is 0
2EI/L: when the magnitudes and signs of end values are identical
User: the user directly enters the initial stiffness if the Input Type is Strength - Stiffness Reduction Ratio.
Elastic Stiffness: elastic stiffness of a member is used as the initial stiffness for inelastic analysis.
Skeleton Curve: when Strength - Yield Displacement is selected for the Input Type, the ratio of the user specified yield strength and yield displacement is used as the initial stiffness.
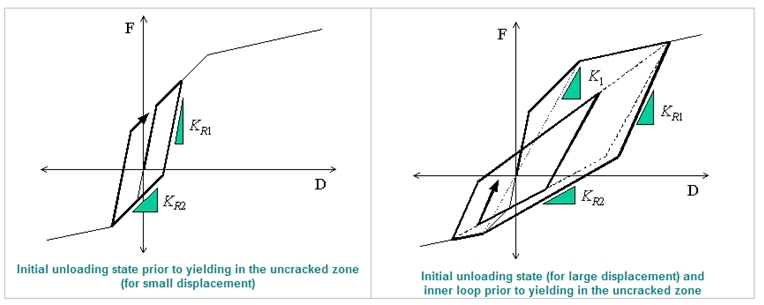
Unloading Stiffness Parameter
Exponent in Unloading Stiffness Calculation: This is an option used to determine the unloading stiffness of the outer loop used in the Clough and Takeda type models among hysteresis models of skeleton curves. This is used to reflect the effect of reduction in stiffness, which occurs as the deformation progresses after yielding. The unloading stiffness is determined by the elastic stiffness reduced by the yield displacement and maximum displacement in the zone where unloading begins and the exponent entered here.
Inner Loop Unloading Stiffness Reduction Factor: This is used to determine the unloading stiffness of the inner loop. The inner loop is formed when unloading occurs before reaching the target point on the skeleton curve while reloading after the loading sign changes in the process of unloading. The unloading stiffness of the inner loop is calculated by multiplying the unloading stiffness of the outer loop by the reduction ratio for the unloading stiffness of the inner loop.
Yield Surface Properties If "P-M in Strength Calculation" or "P-M-M in Status Determination" is selected in Interaction Type, enter the data related to P-M interaction curve and corresponding 3-dimentional yield surface.
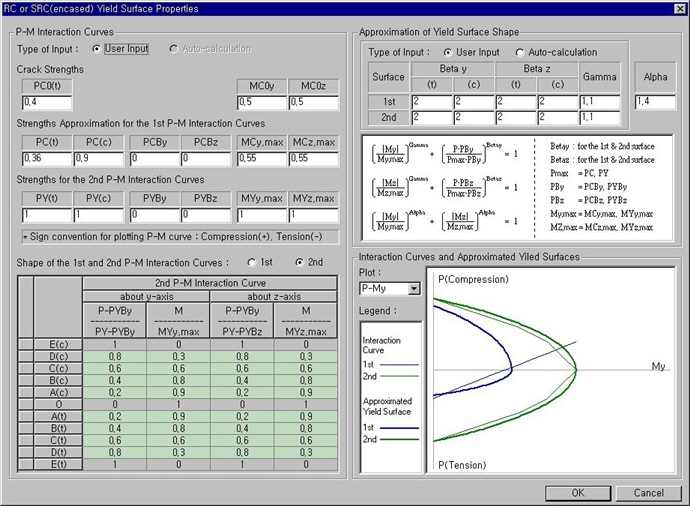
Yield Surface Properties dialog box
P-M Interaction Curves
Enter the P-M interaction curve data required to calculate 3-dimensional yield surfaces. All strength values must be entered with positive sign. Sign convention for plotting P-M curve is positive for compression and negative for tension.
Type of Input: Two input methods, user defined and auto-calculation based on material and section type, are supported to define the variables below. If some items are auto-calculated and the remainder is to be user defined, Auto-calculation should be performed first, and then necessary items can be modified after converting to User Input.
Crack Strengths
NC0(t): Cracking strength due to pure tension force
MC0y: Cracking strength of a section subject to moment about y-axis without the presence of axial force
MC0z: Cracking strength of a section subject to moment about z-axis without the presence of axial force
The following 12 items are required irrespective of the Material Type. But for RC and SRC (encased) sections, approximate NC(t), NC(c), NCBy, NCBz, MCy,max and MCz,max are either entered or auto-calculated on the basis of NC0(t), MC0y and MC0z. All the numerical values are entered as positive.
Strengths for the 1st P-M Interaction Curves
NC(t): First yield strength subject to pure tension force
NC(c): First yield strength subject to pure compression force
NCBy: Axial force at the time of balanced failure in the first yield interaction curve for the y-axis moment of the section
NCBz: Axial force at the time of balanced failure in the first yield interaction curve for the z-axis moment of the section
MCy,max: Maximum bending yield strength in the first yield interaction curve for the y-axis moment of the section
MCz,max: Maximum bending yield strength in the first yield interaction curve for the z-axis moment of the section
Strengths for the 2nd P-M Interaction Curves
NY(t): Second yield strength subject to pure tension force
NY(c): Second yield strength subject to pure compression force
NYBy: Axial force at the time of balanced failure in the second stage yield interaction curve for the y-axis moment of the section
NYBz: Axial force at the time of balanced failure in the second yield interaction curve for the z-axis moment of the section
MYy,max: Maximum bending yield strength in the second yield interaction curve for the y-axis moment of the section
MYz,max: Maximum bending yield strength in the second yield interaction curve for the z-axis moment of the section
Shape of the 1st and 2nd P-M Interaction Curves:
Input the P-M interaction curve shapes. The shape of an interaction curve is defined by coordinates of 11 points among which the furthermost extreme coordinates for tension, compression and flexure are fixed to 0 or 1. Only the remaining 8 points are thus entered. If Material Type is RC or SRC (encased), the interaction curve for the first yield is of a linear shape and as such input is unnecessary. In calculating or displaying the axial component of the coordinates, the sign convention is (+) for compression and (-) for tension.
Approximation of Yield Surface Shape
On the basis of P-M interaction curve, the parameters for 3-dimensional yield surface are either user defined or auto-calculated. If some items are auto-calculated and the remainder is to be user defined, Auto-calculation should be performed first, and then necessary items can be modified after converting to User Input. In case of Alpha, only user defined entry is possible. The value of each parameter is used in the equation of yield surface displayed in the dialog box.
Beta y, Beta z, Gamma: Being the exponential powers of P-My or P-Mz interactions, different values can be entered for the first and second yields. For Beta y and Beta z on the other hand, two separate values representing the ranges of larger and smaller axial forces relative to the axial force at the time of balanced failure can be entered. Alpha: Exponential powers of My-Mz interactions for the first and second yields.
Alpha: Exponent for My-Mz interaction for 1st and 2nd yielding
Coupling of Axial Force & Bending Moments: Select an interaction relationship between the components of axial and biaxial moments. Basically it is assumed that axial force and biaxial moments are inter-related in evaluating the hinge status. Nevertheless, the relationship between the axial force and the biaxial moments can be assumed to be either independent or coupled in formulating the stiffness matrix.
Interaction Curves and Approximated Yield Surfaces
The P-M interaction curves entered by the user or calculated by material and section properties and the 3-dimensional yield surfaces composed from them are displayed. The yield surfaces are displayed by showing the outlines of projection on the reference plane. Through this can we then check how well the P-M interaction curves and the yield surfaces coincide.
Plot: Select an interaction curve or yield surface to be displayed. P-My, P-Mz or My-Mz can be selected.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 button.
button.