The Mohr-Coulomb model is
defined by an elasto-plastic behavior as shown in the
figure below. This behavioral assumption shows reliable
results for general nonlinear analysis of the ground and
is widely used in simulating most terrain.

<Material behavior of
Mohr-Coulomb model>
The Mohr-Coulomb yield criterion has 2 flaws when using
geo-materials. First, the intermediate principal stress
does not affect yield, which is a contradictory assumption
to real soil test results. Second, the Meridian and Failure
envelope of the Mohr-Circle is linear; so the Strength
parameter (angle of friction) does not change with the
Confining pressure (or Hydrostatic pressure). This criterion
is accurate within a limited range of confining pressure
but as the range difference increases, the accuracy decreases.
However, this criterion is often used because it is easy
to use and displays considerably accurate results within
the general confining pressure range.
The major nonlinear parameters used to define the Coulomb
yield criterion are as follows.
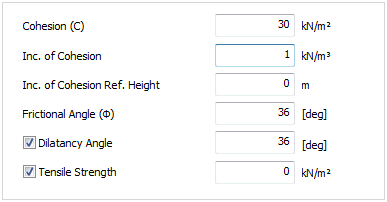
[Cohesion (C) , Friction angle (Φ)]
Soils have different cohesion and friction angle depending
on their type and these values are applied to the shear
strength equation. Soils, unlike other construction materials,
have very little resistance to tension and in most cases
shear failure occurs. When an external force or self weight
is applied, shear stress occurs in the ground. The strain
increases with stress increase and as this progresses,
it works along a plane causing what is known as shear
failure. The shear stress induces shear resistance and
the shear resistance limit is called shear strength. The
shear resistance of soil is made up of 2 comp1nts: cohesion
and friction angle.
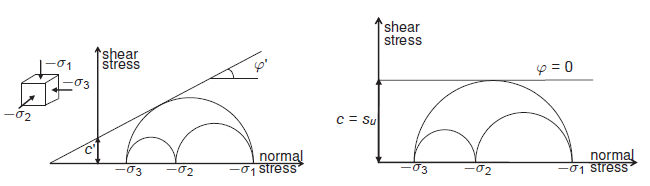
According to Coulomb, the shear strength of soil can
be expressed in the following linear equation.
τ= c + σtanφ(c: Cohesion, σ: Normal stress, φ: Interior
friction angle)
Cohesion is the shear strength when the interior friction
angle is '0(zero)' according to the yield criterion. It
can be defined as an undrained shear strength of cohesive
soils. Sandy soils with no cohesion can be defined as
c=0, but to avoid errors in analysis, it is recommended
that a value of at least 0.2 (kN/m2) be entered.
Defining the cohesion automatically sets the tensile
strength by that amount. However, because tensile resistance
is generally ignored for geo-materials, the Tension-Cutoff
is set to prevent unrealistic resistance behavior to tension.
<Mohr-Coulomb Failure
envelope (Drained/Undrained)>

[Increment of Cohesion Reference Height]
In general, the strength properties of the soil change
with the depth and confining pressure; even within a ground
layer composed of the same material. For example, defining
a soil layer several meters deep as a ‘strength parameter’
may be a limitation in the detailed simulation of a ground
behavior. The ground layer can be further subdivided and
modeled, but this characteristic can be replaced by changing
cohesion according to height. If the cohesion increases
according to the height being '0(zero)', the cohesion
has a constant value and if it is not '0(zero)', the cohesion
is calculated with reference to a standard height (reference
height based on the Global Coordinates) using the
following equation.
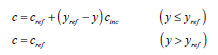
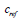 : Input
cohesion value : Input
cohesion value
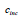 : Incremental
amount depending on cohesion depth : Incremental
amount depending on cohesion depth
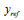 : Depth
of : Depth
of 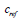 measurement measurement
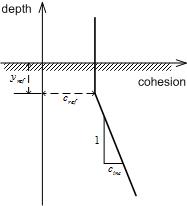
<Conceptual diagram of
cohesion increment>
The 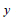 in the equation represent the
integral point positions of an element where the finite
element method calculation occurs. If the integral point
position is higher than in the equation represent the
integral point positions of an element where the finite
element method calculation occurs. If the integral point
position is higher than 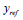 , the cohesion
can be less than 0 in some places. To avoid this, use
the , the cohesion
can be less than 0 in some places. To avoid this, use
the  value instead of further
decreasing the cohesion value. value instead of further
decreasing the cohesion value.
Dilatancy Angle
The dilatancy angle can be viewed as the volume increase
rate according to shear strain. It is a type of strength
parameter for roughness and is generally defined as dilatancy
angle = interior friction angle-30˚. Hence, if the interior
friction angle is less than 30˚, the dilatancy angle is
close to '0(zero)'. In real tests, a negative dilatancy
angle can be defined for vey loose sandy soil but numerically,
the dilatancy angle has a value between 0 and the interior
friction angle.
For undrained analysis, the dilatancy angle must be
set as '0(zero)' when the interior friction angle is '0(zero)'.
The important thing is that the dilatancy angle is a parameter
considered in analysis after changes have been made to
the constitutive equation. If the effects of the dilatancy
angle are not considered, the same value must be entered
for the dilatancy angle and interior friction angle. In
other words, not checking the ‘Consider dilatancy angle’
option automatically performs the analysis with the dilatancy
angle equal to the interior friction angle.
Tensile Strength (Tension-CutOff)
Input the allowable tensile strength of the geo-material.
In many cases, tension cracks can be observed on the natural
ground surface rather than shear failure. Input the allowable
tensile strength to assign tensile resistance to the geo-material.
The tensile resistance of geo-materials are generally
ignored and so the default setting is '0(zero)'. Not checking
the tensile strength option uses a tensile stress, automatically
calculated from cohesion and the interior friction angle,
into the analysis. |