지반 재료를 크게 두가지로 구분한다면, 암반과 토사로 나눌 수 있습니다. 암반은 토사보다 강성이 크며 풍화정도에 따라 강도특성이 달라지고, 응력에 따른 강성 변화가 무시할만큼 작다는 측면에서 거동특성이 구분됩니다. 특히, 암반의 전단강도와 인장강도가 토사에 비해 전체거동특성에 큰 영향을 줄 수 있습니다. Hoek과 Brown은 1980년 jointed rock mass의 파괴에 의한 응력감소현상을 정의하기 위해 등가연속체 개념을 사용하는 방법을 제안하였고, Intact rock과 broken rock을 구분하기 위한 파괴함수를 제안하였으며, 제안된 파괴함수에 의해 암반의 파괴가 정의되면 파괴함수를 정의하는 특정 계수값을 감소시켜 응력감소현상을 묘사하도록 하였습니다. Hoek과 Brown에 의해 제안된 방법은 기존 Mohr-Coulomb 방법이 고려할 수 없는 암반의 일축압축강도를 정의함으로써 암반의 거동을 보다 정확하고 간편하게 나타낼 수 있는 장점이 있으며, 이로인해 현재까지도 암반의 해석에 많이 사용되고 있습니다. 암반의 전단강도는 Mohr-Coulomb의 파괴기준식을 적용하여 나타낼 수 있으며, 특정 응력 범위내에서 Hoek-Brown의 강도정수를 이용하여 Mohr-Coulomb 모델의 점착력과 마찰각을 예측할 수 있습니다.

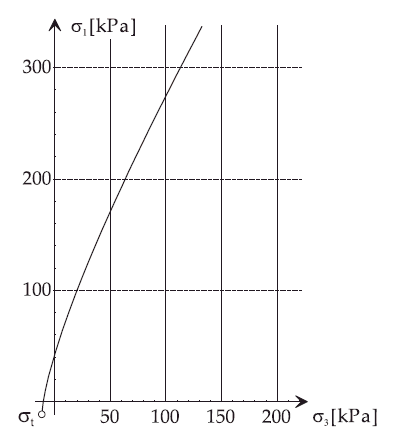
<Hoek-Brown 파괴기준>

Hoek-Brown 기준의 주요 비선형 파라미터는 아래와 같습니다.

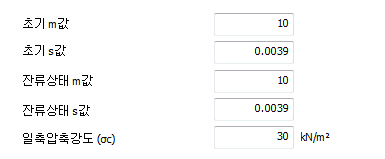
[초기m,s값]

초기 m,s값은 무결암(ntact Rock)의 Hoek-Brown재료상수 중 하나로 암반등급(종류)에 따라 결정되는 경험적인 상수 이며, 일반적인 m값은 아래 테이블과 같습니다.

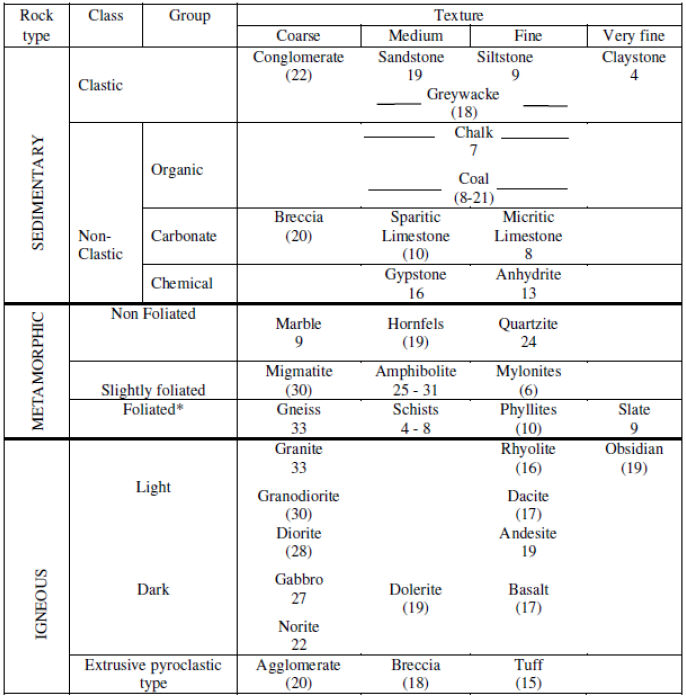
<Hoek-Brown재료상수 m>

s 상수는 무결암일 경우 '1' 을 입력하며 현지 암반의 경우 GSI(Geological Strength Index)로 부터 계산할 수 있습니다. 암반등급에 따른 GSI는 아래 도표와 같으며, 일반적으로 암반분류결과 (RMR,RQD) 로부터 계산하여 예측할 수 도 있습니다.

GSI로 부터 계산된 s는 아래와 같습니다.

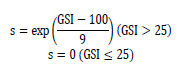
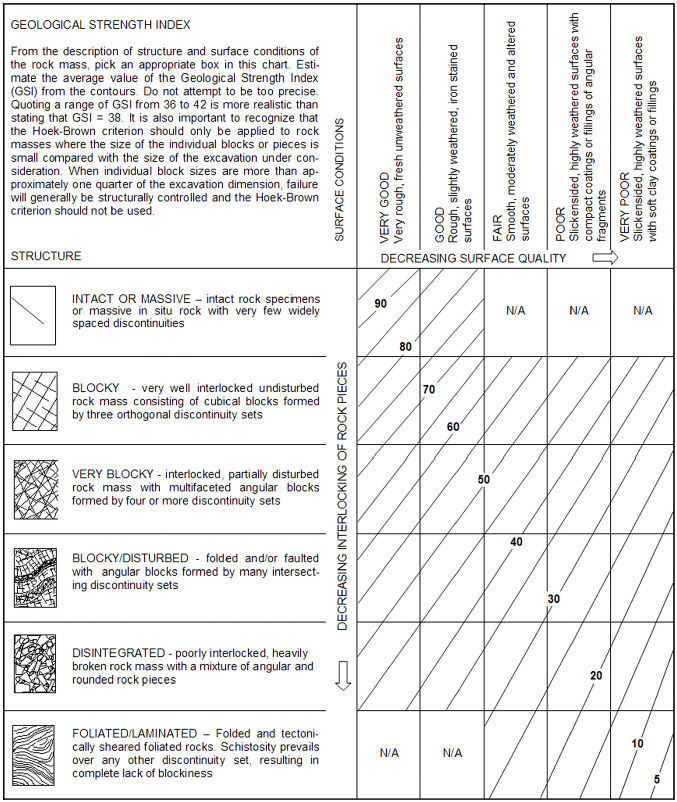
<GSI (Hoek(1999)>

Hoek-Brwon 모델에서 a=0.5인 것으로 간주하며 GSI에 따른 m,s의 관계는 아래와 같습니다.

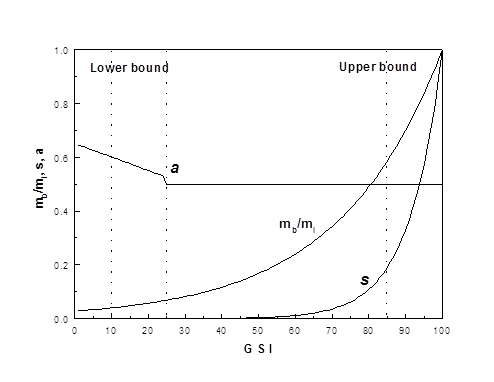
<GSI 와 m,s의 관계>

[일축압축강도]

무결암(Intact Rock)의 일축압축강도 실험 결과를 입력합니다. 암반 등급에 따른 일반적인 수치는 아래와 같습니다.
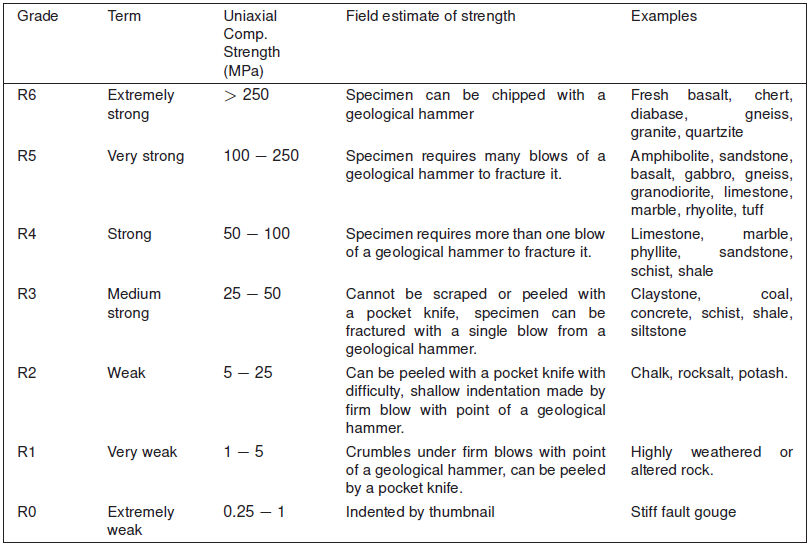