von Mises 모델은 전단응력이 한계치에 도달했을 때 파괴가 일어난다는 원리로써 주로 강재와 같은 연성재료의 거동을 정의하는데 사용됩니다. 이는 지반요소뿐만 아니라 트러스, 매립형 트러스 및 판 요소에도 적용할 수 있으며, 강재로 만들어진 앵커나 네일 및 강관 파일 등을 모사하는 경우 적절히 사용할 수 있습니다.

단, 토질재료에 적용시킬 때 Tresca 기준에서 언급한 바와 같이 인장과 압축강도의 크기가 같다는 점과 정수압에 무관하다는 한계를 가지고 있습니다. 그러나, Tresca 기준과 마찬가지로 포화토의 비배수강도는 von Mises 파괴조건으로 적절히 나타낼 수 있으며, Tresca 기준에서 곡면의 6각형 모서리 때문에 생기는 수학적 어려움과 수치해석의 복잡성이 없으므로 보다 유용하게 사용될 수 있습니다.

- 비선형

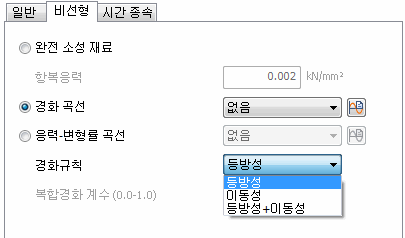
완전소성재료 : 항복응력을 입력합니다.

경화곡선 : 경화곡선은 소재의 소성 특성을 나타내는 재료 물성치로 실험을 통해 얻는 것이 일반적이고, 단축 인장/압축 시험이나 순수 전단 시험 등이 많이 이용됩니다. GTS NX의 경화곡선은 진응력(true stress)-소성변형률 곡선을 입력하도록 구성되어 있습니다. 시험 결과로부터의 변환 과정은 해석매뉴얼(Chapter-4 Materials)을 참고하시기 바랍니다.

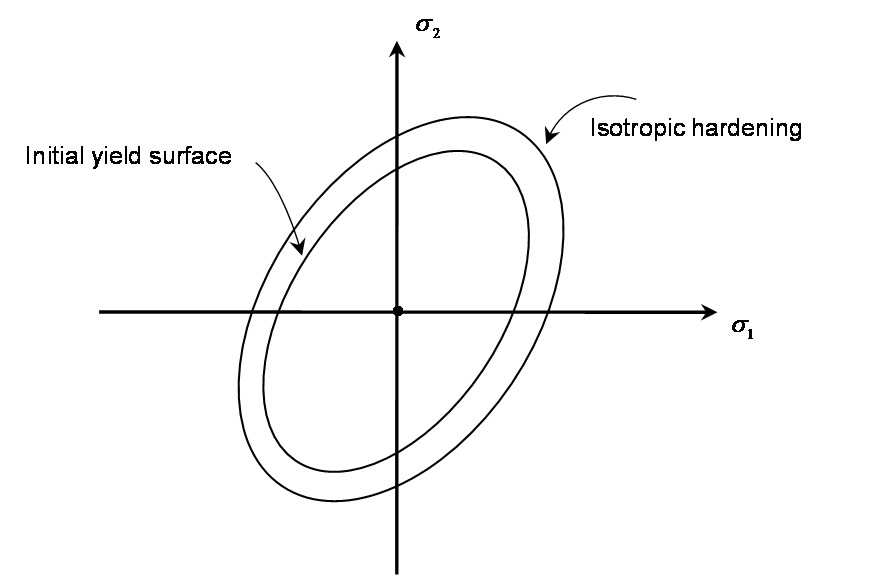
Stress-Strain Curve : Von Mises 항복조건에 대하여 등방성(isotropic) 경화, 이동성(kinematic) 경화, 혼합(combined) 경화 모델을 지원합니다. 등방성 경화 모델은 초기 항복곡면이 균일하게 확장하는 것으로 가정하기 때문에 초기 항복곡면의 중심축이 변하지 않습니다.

등방성 경화모델의 경화인자는 유효소성 변형률(effective plastic strain)로 구성되므로, 경화에 의한 항복응력 또한 유효소성 변형률의 함수로 주어지며, 입력한 경화함수를 그대로 사용합니다.

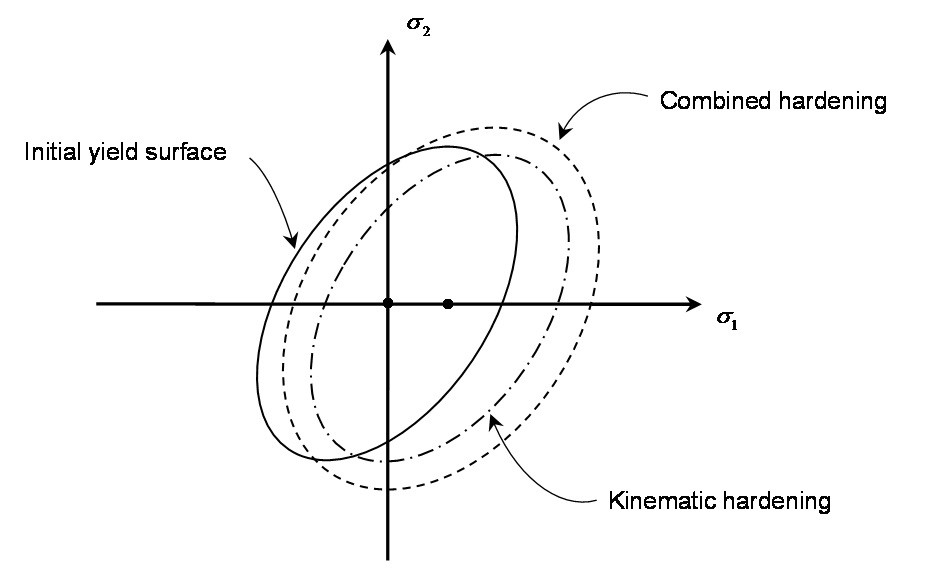
혼합 경화 모델은 소성변형의 발생에 의해 항복곡면의 확장과 이동이 동시에 생겨난다고 가정합니다. 조합 변수(Combined hardening factor, λc)를 이용하여 입력한 경화함수로부터 항복응력을 다음과 같이 산출하며, 조합 변수 λc=0인 경우 등방성 경화에 해당하며, λc=1인 경우는 이동성 경화와 일치합니다.
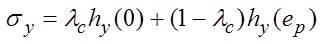