The
figure above is the Analysis control and Result
control setting windows. The additional setting
control options for each analysis type is shown,
and the detailed inputs are listed in the table
below.
Tab |
Linear/Nonlinear
Static analysis |
Construction
stage |
*Consolidation
analysis,
*Fully coupled seepage stress |
Seepage
(Steady/*Transient) |
Slope
stability
(SRM/SAM) |
General |
Water Pressue(Automatic) |
Water
pressure(Automatic) |
Water
pressure (Automatic) |
Maximum
negative pore pressure |
Water
pressure (Automatic) |
In-situ analysis |
Initial
stage(K0)
Final calculation
stage
Specify restart
stage
Restart option
Initial temperature |
In-situ
analysis |
- |
Water
level |
Initial temperature |
Water
level |
Saturation
Effects |
Water level |
Saturation
Effects |
Maximum
negative pore pressure |
Saturation
Effects |
Maximum
negative pore pressure |
Undrained
Condition |
Maximum
negative pore pressure |
- |
- |
Undrained
Condition |
Saturation
Effects |
- |
- |
Maximum
negative pore pressure |
Initial
Configuration |
Nonlinear |
Geometry
Nonlinearity |
Geometry Nonlinearity |
Geometry Nonlinearity |
Load
steps (or
Time Step) |
Load
steps (or
Time Step) |
Load Step (or Time
Step) |
Load steps
(or
Time Step) |
Convergence
Criteria |
Convergence
Criteria |
Convergence
Criteria |
Convergence
Criteria |
Convergence
Criteria |
Advanced
nonlinear setting |
Advanced
nonlinear setting |
Use
arc-length method |
Use arc-length |
Advanced
nonlinear setting |
- |
- |
Advanced
nonlinear setting |
Advanced
nonlinear setting |
- |
- |
- |
Age |
- |
Age |
- |
- |
- |
Seepage |
- |
- |
- |
Initial
condition |
- |
Slope
stability(SRM) |
- |
- |
- |
- |
Geometry
Nonlinearity |
Nonlinear
parameter |
Safety factor |
Advanced
nonlinear setting(Use arc-length method) |
( *
: Time step setting analysis type )
<Table.Static
analysis - Analysis control options for each analysis
type>
Tab |
Eigenvalue,
Response spectrum |
*Linear
time history
(Modal/Direct) |
*Nonlinear
time history,
* Nonlinear time history +SRM |
*2D
equivalent linear |
General |
Initial temperature |
Water pressure
(Automatic) |
Water pressure
(Automatic) |
- |
Water
level |
In-situ analysis |
In-situ analysis |
Eigenvectors |
Water level |
Water level |
Saturation
effects |
Eigenvectors |
Saturation
effects |
Max
negative pore pressure |
Saturation
effects |
Max negative
pore pressure |
Undrained
condition |
Max negative
pore pressure |
Undrained
condition |
Mass parameters |
Undrained
condition |
Mass parameter |
Modal
Damping Ratio |
Mass parameter |
- |
- |
- |
- |
Nonlinear |
- |
- |
Geometry
Nonlinearity |
- |
Converge
standard |
Advanced
nonlinear setting |
Dynamic
analysis |
Modal combination
type |
Damping definition |
Damping
definition |
Effective
shear strain |
Damping definition |
- |
- |
Convergence |
Interpolation
of spectral data |
Interpolation
control |
- |
Mass
parameters |
Slope
stability (SRM) |
- |
- |
Define
time |
- |
Nonlinear
parameters |
Convergence
criteria |
Safety factor |
Advanced
nonlinear parameters (Use arc -length
method) |
(*
: Time step setting analysis type )
<Table.
Dynamic analysis- Analysis control options for
each analysis type>
<Table.
Thermal analysis- Analysis control options for
each analysis type>
Water
Pressure (Automatically consider water pressure)
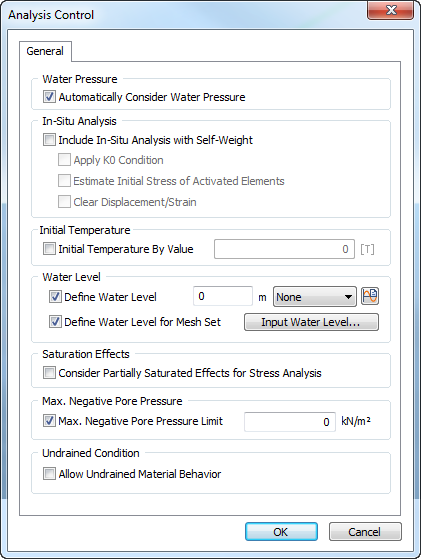 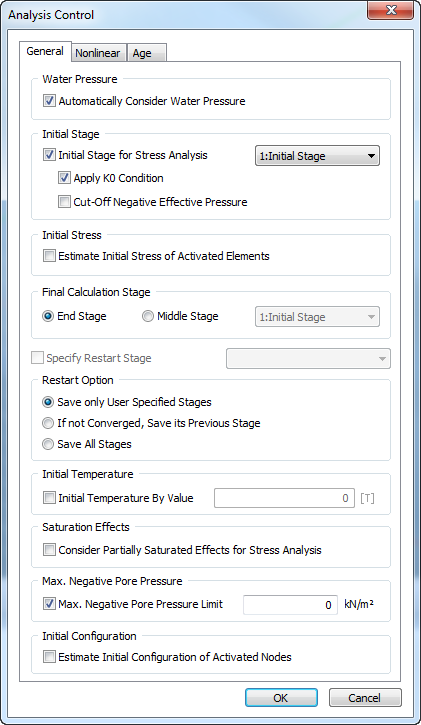
Analysis
Control dialog windows for Linear Static and Construction
Stage analysis types
This option considers all
free surfaces/edges of the model as an external
water pressure. The water pressure is calculated
with reference to the pore pressure acting on
the free surface/edge.
If water level
is set, assume constant water pressure with
reference to the water pressure. If seepage analysis
was conducted previously, use the pore water
distribution (size) calculated for each node. If the pore pressure
is a negative (-) value, water pressure is
not considered automatically
Caution:
If modeling is done for the case where the external
water pressure corresponding to pore water pressure
in the model does not exist, this option needs
to be canceled. When conducting stress analysis
by specifying the water level line, the pore pressure
is calculated by the water level difference between
the free node and corresponding load. Hence, to
accurately examine the influence lines of the
underground water level, Seepage-stress coupled
analysis is recommended.
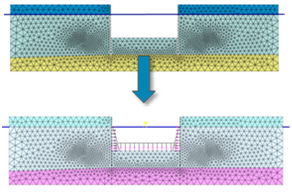
<Application
of auto-water pressure on excavation surface when
excavating below the water level>

In-situ analysis

[Include in-situ Analysis
with Self-weight]
This option resets the
stress state of the singular analysis ground.
The calculated in-situ stress is in equilibrium
with the self-weight and the same boundary conditions
used in singular analysis for analysis. When considering
self-weight in time history analysis, the initial
in-situ stress needs to be calculated. If not,
vibrations can occur due to the load addition.
In particular, the self-load must be included
for nonlinear time history analysis.
[Ko condition consideration]
The 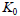 method uses the constant
method uses the constant 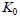 defined by
defined by 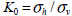 to calculated the horizontal stress from the vertical
stress to set it as the in-situ stress.
to calculated the horizontal stress from the vertical
stress to set it as the in-situ stress.
Using this method, the
vertical stress 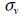 needs to
be found first using self-weight analysis and
that value can be used to compute the horizontal
stress using needs to
be found first using self-weight analysis and
that value can be used to compute the horizontal
stress using 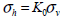 . Here, the shear
stress maintains its value, calculated from the
analysis result. . Here, the shear
stress maintains its value, calculated from the
analysis result.
If the ground surface is
horizontal, there are no problems in using this
method, but if not, the calculated stress state
and self-weight are not in equilibrium.
If the stress is adjusted
without maintaining the equilibrium state, the
stress can change to fit the equilibrium with
the external force in future stress analysis,
even if there are no external force changes, causing
deformation. Hence, the method can be applied
if the additional stress changes are relatively
small. Generally, the conditions when the stress
modification due to the method can be used are
as follows.
When the ground
shape change in the horizontal direction is
small When the pore pressure
distribution shows no change in the horizontal
direction When the horizontal
stress can occur due to the horizontal boundary
condition of the free line/face When using transversely
isotropic materials that have the same material
vertical/horizontal axis
If the 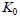 condition is not considered, the stress state
obtained from the self-weight analysis is set
as the in-situ stress. If the ground surface is
horizontal, this method is the same as the
condition is not considered, the stress state
obtained from the self-weight analysis is set
as the in-situ stress. If the ground surface is
horizontal, this method is the same as the 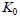 method when method when 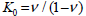 . If not, a horizontal strain exists and different
results than the
. If not, a horizontal strain exists and different
results than the 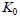 method results
can be obtained. Shear stress also occurs. method results
can be obtained. Shear stress also occurs.
This method is generally
recommended when the ground is sloped. However,
because a value larger than 1 cannot be set for
the 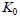 value, a null stage
can be added for re-analysis after using the value, a null stage
can be added for re-analysis after using the 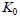 method to calculate the equilibrium
stage, without adding extra external conditions
when a method to calculate the equilibrium
stage, without adding extra external conditions
when a 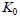 value larger than 1 is needed. However in this
case, the final equilibrium state does not satisfy
the
value larger than 1 is needed. However in this
case, the final equilibrium state does not satisfy
the 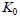 condition. Also, the
modified stress is vastly different from the equilibrium
point, it can be hard to calculated a converging
solution using nonlinearity. condition. Also, the
modified stress is vastly different from the equilibrium
point, it can be hard to calculated a converging
solution using nonlinearity.
Initial
Stress
[Estimate Initial Stress
of Activated Elements]
In
order to calculate the initial stress of ground,
FEA NX perform Linear Analysis even if nonlinear
material is assigned to the elements. In this
case, it can result in, sometimes, over-estimating
the soil behavior (large displacement).
Initial Stress Options can eliminate this problem
especially for newly activated elements which
are to simulate a fill-up ground such as backfill
and embankment.
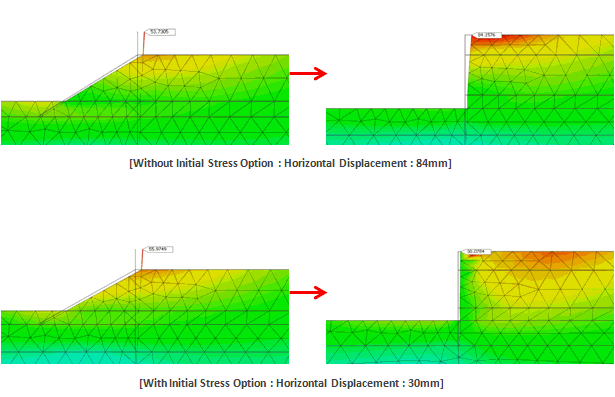
[Engineering
example]
[Clear Displacement/Strain]
The displacement reset
condition may be needed during analysis. For example,
when the displacement and strain due to self-weight
need not be considered in the initial analysis
stage, the reset option can be used to reset the
in-situ state displacement and strain to ‘0(zero)’.
Also, the reset can be
performed at an arbitrary construction stage,
such that the middle stage after analysis of several
stages can be set as the reference state. Displacement/Strain
reset is applied at the end of the specified stage,
after the analysis has finished.
Caution: When conducting
nonlinear analysis by considering geometry nonlinearity,
arbitrarily modifying the deformation does not
guarantee the continuity. Hence, this option is
not recommended for geometric nonlinear analysis
of construction stages.
[Cut-Off Negative Effective
Pressure]
When conducting linear static analysis for initial
stress of ground, tensile stress can be generated
especially at the ground surface according to
the geometry and stiffness differences. In this
case, this tensile stress can take effect on the
convergence for the following stage (nonlinear
analysis) significantly. If there is tensile
stress generated in in-situ state, software will
make it close to Zero to ignore the abnormal stress
distribution. Since this is the basic concept
of initial stress of ground, strongly recommended
to use for all staged analysis.

Initial Temperature

This option sets the initial
temperature of the single analysis model. If not
checked, the initial temperature defined in the
[Analysis Control] is considered. The temperature
is used to assess the effects of thermal load,
and the temperature difference with the input
temperature load is considered in the analysis.
Water Level
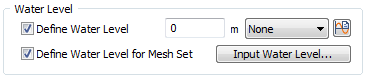
[Define water level]
Directly input the water
level height, or select a water level function
that already has a specified water level to set
the water level. The set water level is applied
to the total model. When using the water level
function, the input value is multiplied to the
function value and applied.
[Define water level for
mesh set]
Define the
water level for each mesh set.
If the groundwater
layer is surrounded by rocks or an impermeable
clay layer (confined aquifer), the presence/absence
of the groundwater level for each ground layer
can be set for analysis.
If the total
groundwater level is input and a mesh set has
a defined groundwater level, the mesh set groundwater
level has priority and the total groundwater level
is applied to mesh sets that do not have a defined
level.
If
the water level and the function are specified
at the same time, the input water level and the
function are multiplied and reflected in the analysis.
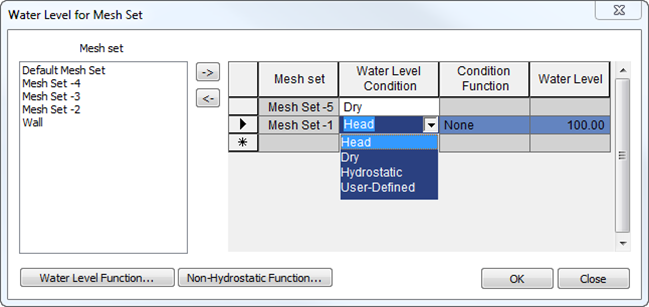
Mesh Set
– select the mesh set to apply the water level
condition.
Water Level
Condition – select between Head, Dry, Hydrostatic
and User-Defined for applying water pressure
Head – compute
head according to the water level assigned to
the mesh set.
Dry – assume
there is no pore water pressure applied to the
mesh set.
Hydrostatic
– assign a non-hydrostatic water pressure to a
mesh set.
User-Defined
– apply a user-defined pressure gradient to a
mesh set
Condition
Function – select a condition function for Head,
Hydrostatic & User-Defined
- None – set a single
water level for water pressure calculation.
- Water Level Function
– assign a function which describes the water
level using General Function in 2D and Surface Function
in 3D.
- Hydrostatic
– not available
- Water Level Function
– assign a Non-Hydrostatic Water Pressure function
type Hydrostatic to define a pressure profile
to be used to compute the water pressure.
- Water Level Function
– assign a Non-Hydrostatic Water Pressure function
type User-Defined to apply a linear pressure profile.
Water Level
– input water level to be considered for the selected
mesh set (only for Head).
Saturation Effects

This option is to conduct
accurate analysis when the saturation has a value
between the unsaturated state (Se=0) and the saturated
state (Se=1). The partial saturation can be applied
in the following two cases.
Applying the partial
saturation to calculated the effective stress-total
stress relationship (Use Bishop’s effective
stress relationship equation) Consider the partially
saturated state in the unit weight calculations
for a material, such that the unit weight
when partially saturated has a value between
the saturated unit weight and unsaturated
unit weight.
If partial saturation is
not considered, Terzaghi’s effective stress formula
is used and the unit weight is set as either the
saturated unit weight or the unsaturated unit
weight, depending on the pore water pressure distribution
(a value in between is not used.). The saturation
is defined as a function of pore water pressure
and if partial saturation is considered, the unsaturated
properties of the material need to be defined
to define the saturation function for pore water
pressure.

Maximum negative pore water pressure limit

This option limits the
maximum negative pore pressure by the input number.
If partial saturation is not considered, Terzaghi’s
effective stress formula is used and the pore
stress of the unsaturated state can be overly
reflected in the calculation. Hence, when not
considering partial saturation, the negative pore
water pressure needs to be limited to a certain
value. Reversely, if the partial saturation is
considered, Bishop’s equation is used and there
is no such danger. In other words, the pore stress
is limited by the unsaturated property function
and there is no need for a particular limit on
the negative pore water pressure.
Construction
stage general setting
[Initial stage]
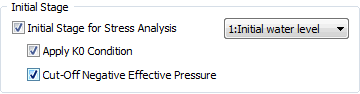
Specify the construction
stage that will be considered as the in-situ condition
and check the Ko consideration. Refer to the ‘Linear
analysis’ option for more information on the Ko.
The displacement and strain for the construction
stage specified as the initial stage, is reset.
[Initial Stress]

In
order to calculate the initial stress of ground,
FEANX perform Linear Analysis even if nonlinear
material is assigned to the elements. In this
case, it can result in, sometimes, over-estimating
the soil behavior (large displacement).
Initial Stress Options can eliminate this problem
especially for newly activated elements which
are to simulate a fill-up ground such as backfill
and embankment.
[Final
calculation stage]

The default setting is
calculation up to the final stage, but a separate
Final calculation stage can be set when stopping
the analysis to check the interim results.
[Specify
restart stage]
When specifying the construction
stage, the [Specify restart stage] option can
be checked on the Analysis control for each stage.
The checked stage is automatically saved on a
separate result file and when the same model is
used for re-analysis, the re-analysis can be performed
starting from the next stage of the result file.
It is useful when many construction stages are
specified.
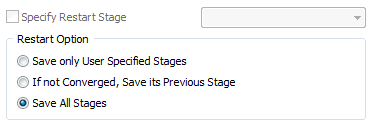
[Restart
option]
If the converge standard
is not satisfied for non-linear analysis, the
reliability can be in question and so, it is important
to check whether the converge standard is satisfied
for each stage during construction stage analysis.
In particular, because construction stage analysis
can take longer time than single analysis, the
[If not converged, save its previous stage] option
is available when a stage does not satisfy the
standard. This option saves the stage before as
a result file and the model can be review and
modified before restarting. Also, the [Save all
stages] option is available for when the analysis
is terminated forcefully, due to the computer
system instability or to check the interim results.
However, because saving all analysis results takes
up a large size, the save capacity needs to be
secured on the computer.

Initial Configuration

During
construction, the newly activated nodes(elements)
can be set to the position considering deformed
shape in the previous stage. Following is the
example of staged embankment to compare the settlement
distribution between with and without applying
the option.
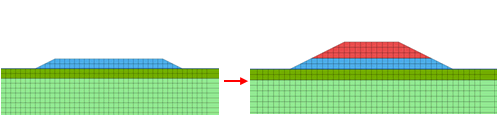
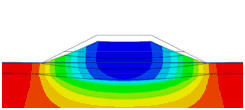 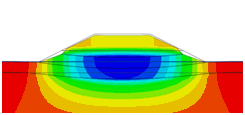
[With
option vs
Without option]
Geometry Nonlinearity

In
case of large deformation analysis, the user can
check more reasonable behavior with this option.
This is to consider geometric nonlinear effects
in stress, fully coupled and slope stability analysis.
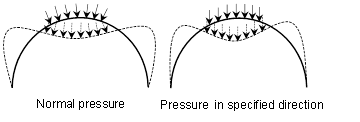
Analysis can take into account load nonlinearity
which is reflecting the effects of follower loads,
where the load direction changes with the deformation.
Depending on the deformed shape, the pore water
pressure can be updated automatically.
Load steps (or Time Steps)
A static load can be used
for nonlinear static analysis. The defined load
sum can be applied at once or in stages, as an
increment, cumulatively. If the load increment
is too large, it may be hard to calculate the
converging solution and if the load increment
is too small, unnecessary is spent on calculations.
In case of considering time-dependent material,
the user can define Time steps to check the results
with time elapse.
Convergence Criteria
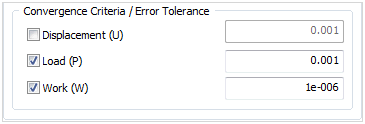
Because nonlinear analysis
uses iteration methods, the converge condition
can be used to determine whether the solution
has converged. The convergence is determined by
comparing the displacement, member force or energy
change in the previous calculation with the reference
values. If all selected conditions are satisfied,
the iteration is determined to have converged.
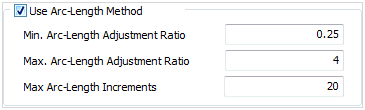
Use Arc-Length
Method
FEA NX uses the Newton-Raphson
method, where the increments are calculated to
minimize the error repeatedly, as a base for calculating
the nonlinear analysis solution. The Full Newton-Raphson,
which renews the stiffness matrix for each repeated
calculation, is basically used and the Newton-Raphson
method or Initial stiffness method can be used
at the renewal point. Also, other various options
such as the line search method to improve the
convergence, or arc length method, to calculate
the unstable equilibrium state, can be used (Refer
to Chp.5-5 of the Analysis manual for more details).
The iterated calculation method repeats the calculation
until a satisfactory solution is obtained. If
there is no accurate numerical basis, the initial
setting value is recommended.
[Minimum arc-length adjustment
ratio]
Input the minimum change
to the initial arc length to current increment
arc length ratio. This prevents the arc length
from becoming infinitely small.
[Maximum arc-length adjustment
ratio]
Input the maximum change
to the initial arc length to current increment
arc length ratio. This prevents the arc length
from becoming infinitely large.
[Maximum arc-length increments]
Input the maximum number
of increments. Nonlinear analysis using the explicit
arc length method is conducted until the load
factor is larger than 1, or when the number of
increments reaches the maximum value. The explicit
arc length method may not work, according to the
load in the problem, and the number of maximum
allowable load increments is input to prepare
for this.

Advanced
nonlinear setting
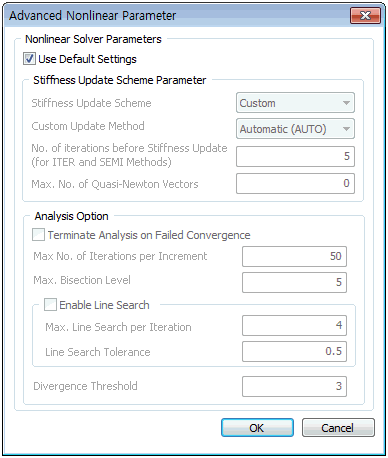
The basic settings use
the nonlinear analysis parameters and the [Use
default settings] option is selected for most
problems. The detailed settings are as follows.
[Stiffness update scheme
parameter]
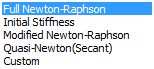
The Full Newton-Raphson,
which renews the stiffness matrix for each repeated
calculation, and the Initial stiffness method,
which maintains the initial stiffness matrix and
has very weak nonlinearity, are available. Other
options such as the Modified Newton-Raphson method
or Secant method, which increases the convergence
and efficiency of the Newton-Raphson material
properties, can be selected. Refer to Chp.5 of
the Analysis manual for more details on the algorithms.
The user can also specify a method to recompose
the stiffness matrix by selecting repetition,
semiautomatic and automatic.
[Analysis option]
Terminate Analysis
on Failed Convergence : Close analysis when
convergence fails. If the option is not selected,
the analysis is continuously conducted even
when the values to not converge. Max number of Iterations
per Increment : Input the maximum number of
iterations for one increment. [Maximum Bisection
level] : Specify the maximum division level. Enable Line Search
: Use the line search feature. This feature
is helpful for problems with flexible structures,
where the stiffness increases with the load,
or if the nonlinear analysis solution converges
while vibrating. It may only increase the
analysis time when used on an ineffective
problem. Max Line Search
per Iteration : Input the maximum number of
line search per repeated calculation. Line Search Tolerance
: Input the line search tolerance. Divergence Threshold
: Specify the number of allowable diversions
if the value does not converge. The modified
Newton-Raphson method renews the stiffness
matrix at the start of each load increment.

Age
In case of construction
stage analysis, the user can take Age into account
to consider creep / shrinkage effect generated
in the previous stage. For the time-dependent
material, the user, in general, can enter the
curing period of concrete.

Initial
condition (Seepage)
This option specifies the
initial pore water pressure distribution in the
ground for transient seepage analysis. The initial
conditions must be set for the transient analysis.
The initial condition can be selected by using
the values at time ‘0(zero)’ of the transient
time step, using an arbitrarily set water level
height, or using the water level function.
Safety factor (SRM)
Input the initial safety
factor and the safety factor increment for each
repeated calculation step. The resolution of safety
factor can also be set.
[Resolution of Safety Factor]
- Slope analysis using SRM uses the strength reduction
method, and the resolution of safety factor value
can be input to specify the accuracy of the safety
factor calculation. The resolution of safety factor
is used as a convergence standard for stability
analysis. However, if the resolution of safety
factor is entered too low, the analysis time increases
greatly and so, the following guideline needs
to be used to input an appropriate value.
Safety factor
accuracy |
Applicability |
0.05 |
Low(Use
as initial review) |
0.01 |
Average |
0.005 |
High |
<Table.
Dynamic analysis- Analysis control options for
each analysis type>

Eigenvectors
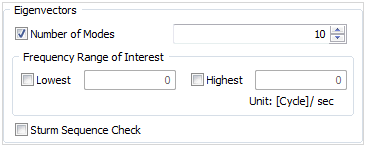
Input the number of natural
frequency modes (number of modes) to input and
specify the range to search. The option to check
for any omitted eigenvalues can be applied.
Mass parameters
[Coupled Mass Calculation]:
Use a mass matrix that considers the coupling
between modes. Check to use a consistent mass
matrix, and uncheck to use a lumped mass matrix.
It is hard to determine which is more accurate,
but for eigenvalue analysis, using a lumped mass
matrix displays a more flexible behavior than
using a consistent mass matrix.
Modal
Damping Ratio
Calculate
Strain Energy Proportional Damping Ratio
Eigenvalue
analysis provides damping ratios for each mode
based on the strain energy of the structure.
This
can
be used to obtain modal damping
ratios
in
the
structure
with different materials or damping devices. The
modal damping ratio can be found after analysis
from Result
>
Advanced
>
Others
>
Modal
Damping Ratio.
Modal combination
type
If the maximum actual physical
quantity is assumed to be the maximum physical
quantities (maximum values for displacement, stress,
member force, reaction force etc.) of each mode,
the maximum values of each mode can simply be
added. But because there is no guarantee that
the maximum values of each mode occur on the same
time step, it is difficult to express the maximum
actual physical quantity through simple linear
super positioning.
Hence, a mode combination
method to approximate the maximum value is needed.
Various mode methods are suggested, but because
no one combination can give the appropriate approximation
for all cases, the characteristics of each mode
combination needs to be understood. The modal
combination types are as follows, and refer to
Ch.5 of the Analysis manual for more detailed
algorithms.

This method assumes
that all mode responses occur on the same phase
and the maximum value for each mode is judged
to occur on the same time step, giving the most
conservative results.
This method provides
appropriate results when each mode is sufficiently
separated.
This method removes
one mode( ) that has the maximum absolute value
from the SRSS method, and like the SRSS method,
this method provides appropriate results when
each mode is sufficiently separated.
This method includes
effect of adjacent frequency modes in the SRSS.
In other words, if two mode frequencies satisfy
the following, the two modes are determined to
be adjacent, within 10% of the frequency.
If the cross-correlation
coefficient between modes is 1, it displays the
same results as the SRSS method.

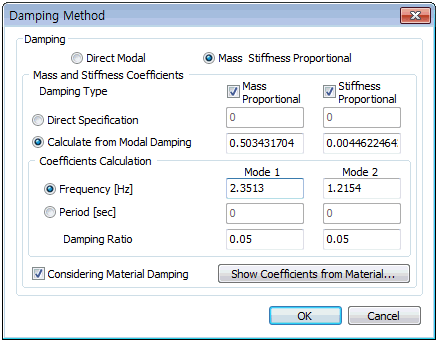
Damping definition
[Direct modal]
The user directly defines
the damping ratio of each mode, and the mode response
is calculated using that ratio. The direct modal
method is only activated for Response spectrum
/ Time history (Modal) analysis.
Define the default
damping ratio that is applied to all modes, except
for the ones defined by the user. The default
damping ratio is applied to all modes that have
a lower priority than the specified mode. If the
input damping ratio is different from the damping
ratio of the response spectrum function, the spectrum
data is adjusted with reference to the input damping
ratio and used for analysis.
It is used to directly
input the damping ratio for each mode. The mode
number and mode damping ratio are input separately
and then added.
[Mass Stiffness Proportional]
Compute the damping constant
for mass proportional attenuation and stiffness
proportional attenuation. The proportional coefficient
can be directly input, or automatically calculated
from the mode attenuation, for checked items on
the attenuation type.
Input the mode frequency
or period and specify the damping ratio to automatically
calculate the proportionality coefficient.
Here, the attenuation for
each material, when calculating the mass &
stiffness coefficients from the modal damping,
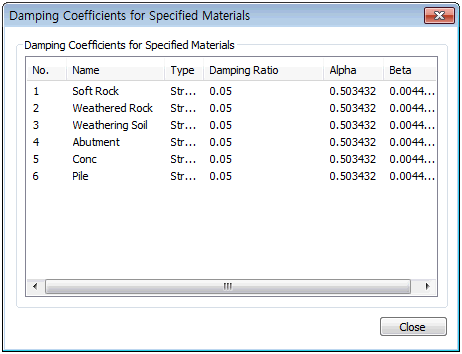
can be reflected in the analysis. The damping
ratio of each material, input in the [Show Coefficients
from Material], and the damping coefficient (alpha,
beta) of the damping matrix, calculated using
that value, can be checked.
Interpolation
of Spectral Ratio
Select the interpolation
method for the response spectrum load data. Both
linear interpolation or logarithmic interpolation
can be used for the spectrum data period and the
default setting is the logarithmic interpolation
method. If multiple damping ratios are in the
spectrum data, interpolation of the damping ratio
also follows this option. Spectrum data with one
damping ratio cannot be interpolated and is corrected
using the following equation. (1.5/(40xAttenuation+1)
+ 0.5)

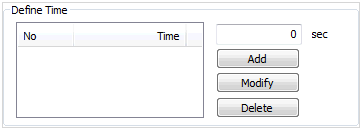
Define Time (Nonlinear time history + SRM)
Specify the time to view
the SRM analysis results. Multiple time steps
can be specified. The SRM stability assessment
is conducted using the nonlinear time history
stress results from the specified time period.
Effective shear strain (2D equivalent linear analysis)
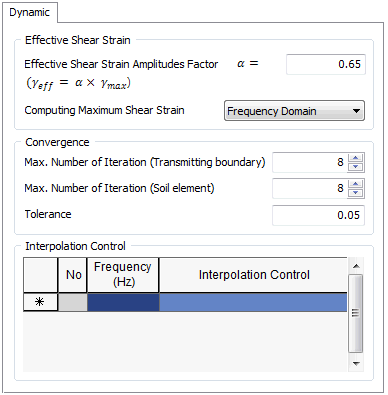
The shear strain of the
ground changes with the input seismic motion or
vibration load. To apply equivalent linear analysis,
the concept of effective shear strain is introduced,
and the material properties are simplified to
have equivalent linear values for calculation.
Frequency domain analysis
is analyzed to have a certain shear modulus and
damping for each frequency, and the material nonlinearity
cannot be considered. Hence, the 2D equivalent
linear analysis uses iterated calculations, using
the changing ground stiffness and damping ratio
due to the shear strain calculated in the previous
stage, to consider the nonlinear behavior of the
ground. Here, the maximum shear strain used in
the previous stage is multiplied by a certain
value(50%~70%) smaller than 1 to define the effective
shear strain. The effective shear strain is used
because the maximum shear strain generates a larger
strain energy than the actual behavior.
Generally, an effective
shear strain coefficient of 0.65 (65%), or the
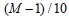 value that uses the earthquake
magnitude is used. Also, a maximum shear strain
calculation method in the time domain is supported
to calculate shear strain more precisely than
the maximum shear strain found using the RMS(root
mean square) in the frequency domain. value that uses the earthquake
magnitude is used. Also, a maximum shear strain
calculation method in the time domain is supported
to calculate shear strain more precisely than
the maximum shear strain found using the RMS(root
mean square) in the frequency domain.
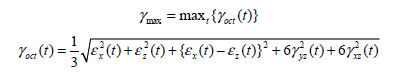
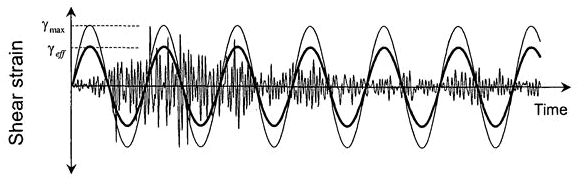
<Difference
between maximum and effective strain>
There are two methods to
calculating the maximum shear strain; the time
domain and frequency domain. The time domain method
defines the load (acceleration, force etc.) changes
according to time and composes the structural
state as a differential equation. Hence, the structural
response (displacement, velocity, acceleration
response) can be calculated by performing the
integration for every time interval. The frequency
domain method is useful when determining the relationship
and ratio between the load response and frequency
characteristics. Because it is hard to determine
this relationship and ratio for irregular waves
such as earthquake response, the wave in the time
domain is converted to the frequency domain and
used for analysis.
[Interpolation control]
Input the frequency range
for frequency domain analysis. Interpolation methods
are used to efficient frequency domain analysis
and one of the four methods can be selected.

Select [Coupled Mass Calculation]
to conduct the analysis for all frequencies and
if the interval is specified, the analysis frequency
interval in the frequency domain becomes the set
interval. |
