|
The Response spectrum analysis uses and combines the spectrum data, corresponding to the absolute maximum values of the time response for each mode, using the principle of superposition. Because the simultaneity of the maximum value occurrence for each mode is not considered and only the absolute maximum values are combined, it is considered as an approximate solution to the Modal linear time history analysis. However, the correlation between modes is considered in the mode combination to correct for simultaneity errors.
Spectrum data
A spectrum data is the absolute maximum displacement (or velocity, acceleration) values found by fixing the damping ratio and changing the period (mass, stiffness) of a single DOF system for a time history data. Because the damping ratio for each mode of the structure can be different, instead of using a spectrum data for one damping ratio, multiple spectrum data for different damping ratios are created and interpolated for the damping ratio. The period spacing used to create the spectrum data can be different to the natural period of the structure and so, interpolation for the natural period is also needed. Both linear interpolation and logarithmic interpolation are supported. Also, the spectrum data generally uses the design response spectrum created from the statistical historic earthquake data in the target region, rather than converting a particular given data. Because a design response spectrum with one damping ratio is generally used, correction instead of interpolation is applied for this case.
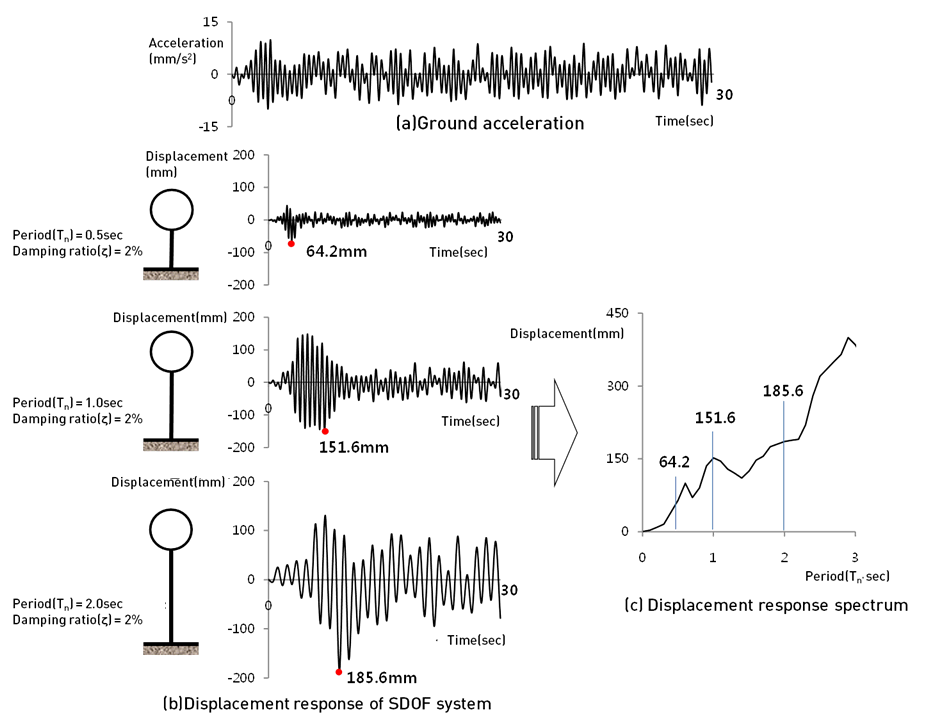
<Create displacement response spectrum of SDOF system>
Damping consideration
Damping consideration is essential for accurate dynamic analysis. All real structures cannot vibrate infinitely and the energy loss at the molecular level, or energy loss in the structure due to interaction between component elements, applies damping to the system and gradually decreases the vibrations of the structure.
In particular, for stimulation near the natural frequency region (resonance effect) of the structure, damping has a dominant effect on the analysis results.
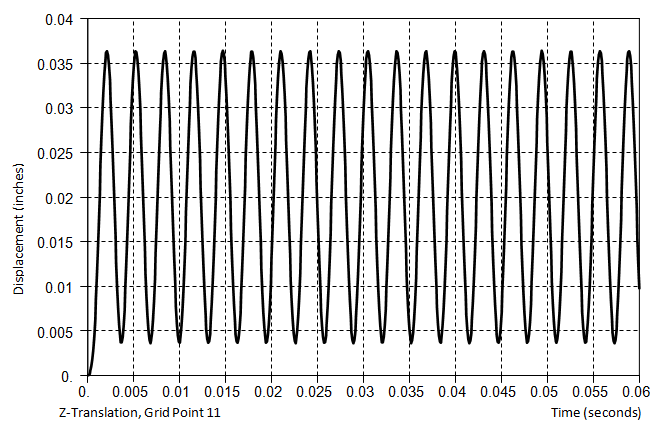 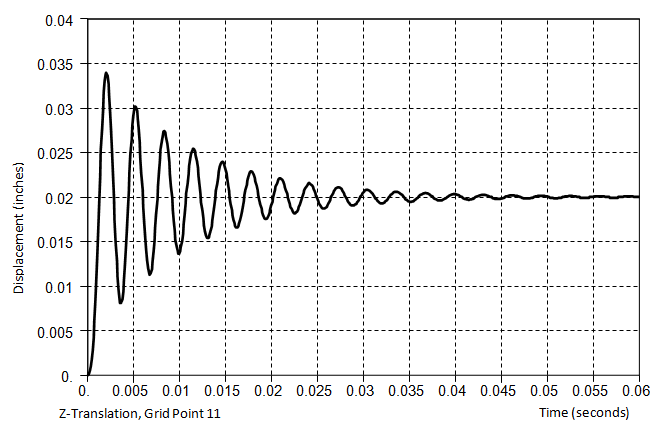
<Without damping> <With damping effects>
The accurate damping ratio of the structure needs to be determined through experimentation, and the generally used damping ratios used are as follows.
|
System
|
Damping ratio
|
|
Steel (within elastic region)
|
< 1 %
|
|
Steel structure with joint
|
3 % ~ 7 %
|
|
Pipe system with small diameter
|
1 % ~ 2 %
|
|
Pipe system with large diameter
|
2 % ~ 3 %
|
|
Rubber material
|
~ 5 %
|
|
Prestressed concrete structure
|
2 % ~ 3 %
|
|
RC structure
|
4 % ~ 7 %
|
The modal damping is most frequently used to express the structural damping for general numerical analysis. The modal damping determines the damping for each natural frequency in the system and can be largely divided into proportional and non-proportional damping. Proportional damping can use the mass proportional type, stiffness proportional type or Rayleigh type damping.
Mass proportional damping expresses the viscous damping due to external factors such as air resistance and assumes that the damping matrix is proportional to the mass. For stiffness proportional damping, the dissipation damping effect (vibration energy dissipated to the ground) is hard to express directly and is assumed to be proportional to the damping stiffness. Hence, the damping can be overestimated at higher modes.
Rayleigh damping is the stiffness proportional type corrected for the damping constant at higher modes and can be expressed as the sum of the mass proportional type and stiffness proportional type.
|
