The von Mises model is often
used to define the behavior of ductile materials based
on the principle that yielding occurs when the shear stress
reaches the threshold value. This model can be applied
to truss, embedded truss and pipe elements as well as
geotechnical elements. It can also be applied when simulating
anchors, nails or steel pipe piles made from steel.
The von Mises model has the same limitation as the Tresca
model when applied to soil materials; it does not consider
the effects of hydrostatic pressure and the yield stress
is the same for compression and tension. Like the Tresca
criterion, the undrained strength of saturated soil can
be appropriately presented using the von Mises yield criterion.
This model is useful because it does not have the mathematical
difficulty or analysis complexity caused by the hexagonal
corners of the curved surface on the Tresca criterion.
As the material yields hardening
defines the change of yield surface with plastic straining,
which is classified into three types : Isotropic, Kinematic and Combined.
Appropriate for all types of
materials, which exhibit Plastic Incompressibility.
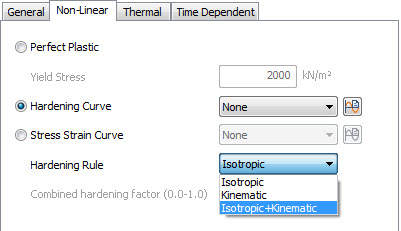
Perfect Plastic: Specify Initial Uniaxial
(tensile)
Yield Stress
Hardening Curve : Relation between plastic strain
and stress true stress) can be resulted from
uniaxial
compression
/ tensile test or shear test.
Stress Strain curve (optional)
:
Relation between strain and stress true stress)
Hardening Rule: Isotropic, Kinematic and Combined
(Isotropic + Kinematic)
-
Total
increment of Plastic can be expressed by Isotropic
and Kinematic Hardening as
follows:
-
Combined hardening factor
(λc, 0~1)
represents the extent of hardening. ‘1’ for Isotropic,
‘0’ for Kinematic, and between ‘0~1’ for Combined
hardening.
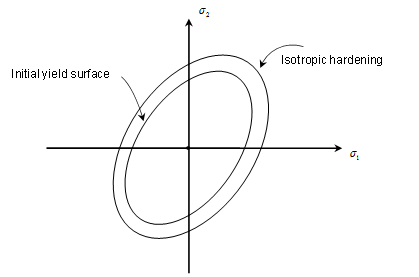 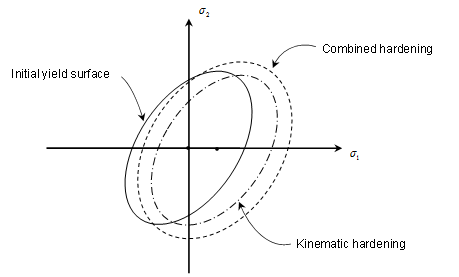
[ Yield Surface for each hardening
rule ]
|
