일반 함수 (공간)
전체
직교 또는 원통 좌표계 기준으로 공간 상의 위치 (좌표) 변화에 따른 값의 변화를
함수로 설정하고 이를 하중 설정 시 활용할 수 있습니다. 수위 조건의 경우 화면 상의
선을 선택하여 바로 지정할 수 있지만, 좌표 변화에 따른 수위를 함수로 등록하면 이를
시공단계에서 수위선으로 활용할 수 있습니다.
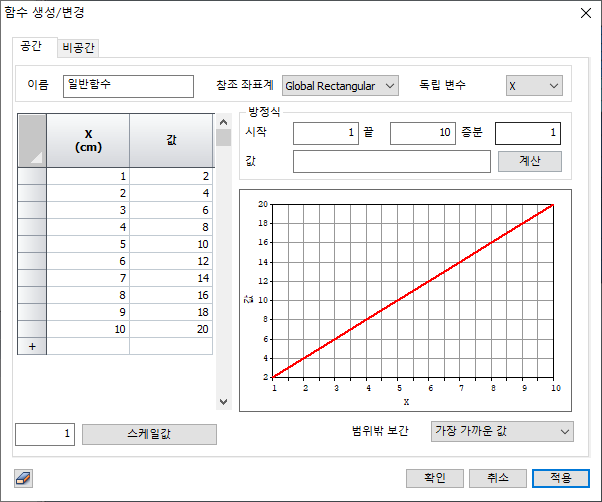
참조 좌표 성분에 따른 독립 변수 (X, Y,
Z 또는 R, TH, Z)를 설정하고 설정된 변수에 따른 값을 테이블에 입력하여 함수를
생성합니다. 미리 만들어진 함수를 엑셀로부터 복사+붙여넣기 할 수 있습니다.
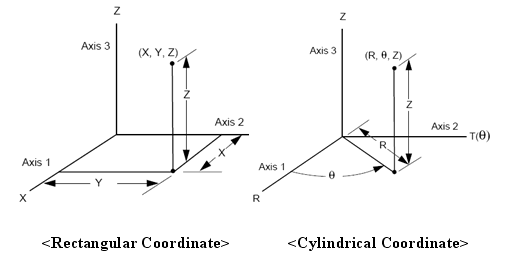
<참조좌표계 기준>
[방정식]
독립 변수에 대한 값을 직접 정의하지 않고
방정식을 이용하여 지정할 수 있습니다.
예를
들어, 직교 좌표계에서 Y=2*X 와 같은 함수를 설정할 경우, X 좌표 범위 (시작,
끝)를 지정하고 함수값을 계산할 X 좌표 증분을 입력한 후 값에 2*X 를 입력하고
계산 버튼을 선택하면 위 그림의 예시와 같은 함수가 자동 생성됩니다.
원통
좌표계의 경우 T 좌표 기준으로 일정 각도 사이에 Sin(T)의 함수를 정의할 경우,
각도 범위 (시작, 끝)과 증분 각도를 입력한 후 값에 sin(T)를 입력하면 정해진
각도 범위 내에서 sin 함수가 생성됩니다.
[스케일 값]
초기값은 1로 설정되어 있으며, 정의된 함수값에
곱해져서 사용되는 값 입니다. 예를 들어, 정의된 모든 함수값을 2배로 증가시킬 경우
스케일 값에 2를 입력합니다.
[범위 밖 보간]
함수의
독립 변수 범위 밖 벗어난 값에 대한 함수값을 설정하는 방법입니다. 정의된 구간 이외의
함수값을 0으로 설정할지, 가장 가까운 변수의 함수값을 동일하게 사용할지, 혹은 선형
보간하여 사용할 지를 결정할 수 있습니다.
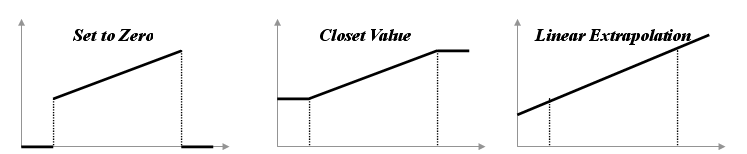
<Extrapolation>

일반
함수 (비공간)
전단 강성 및 스프링 강성을 함수로 지정할
경우 사용합니다. 상대변위 vs 힘/면적은 전단 강성 함수로 사용되며, 상대 변위
vs 힘/길이는 스프링 강성 함수로 적용됩니다.
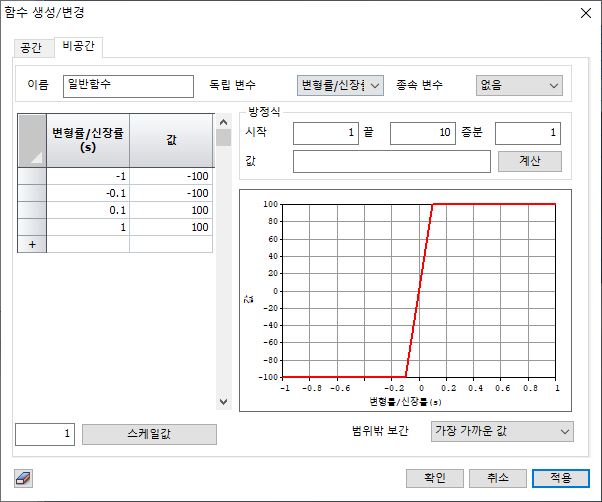 

일반화 공간 함수
일반 함수 (공간)과 사용 목적 및 기능은
동일합니다. 단, 일반 함수 (공간)의 경우 독립 변수 축을 하나만 설정하는 1차원
공간 함수 이지만, 일반화 공간 함수는 세 축 모든 방향을 고려한 함수를 생성할 수
있습니다. 입력 방식 및 세부 기능은 일반 함수 (공간)과 동일합니다.
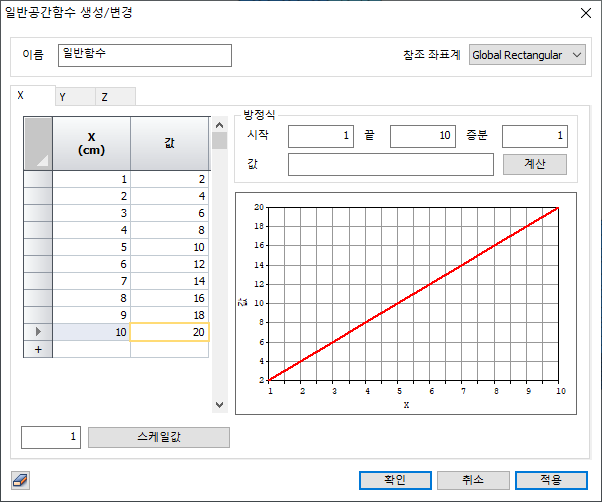
참조
좌표 성분에 따른 독립 변수 (X, Y, Z 또는 R, TH, Z)마다 각 축 방향에
대한 값을 테이블에 입력하여 함수를 생성합니다. 미리 만들어진 함수를 엑셀로부터 복사+붙여넣기
할 수 있습니다.

곡면
함수
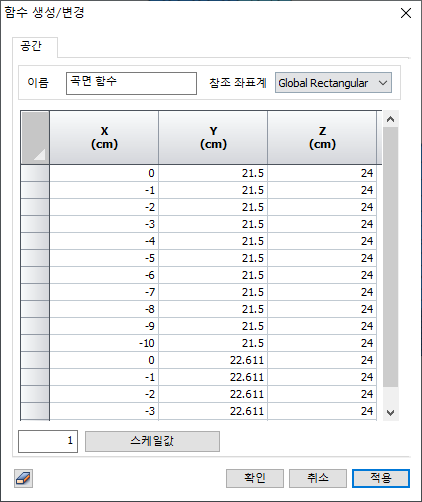
3차원
공간 상의 수위면을 지정하는 함수입니다. 아래 테이블과 같이 전체 또는 원통 좌표계
기준으로 변수에 대한 값을 정의하여 3차원 수위면을 생성할 수 있지만, 경계 조건>수위
조건 기능에서 모델 상의 면을 직접 선택하여 아래와 같은 좌표 정보가 자동 추출된
수위면을 정의할 수 있습니다. 여기서 X 좌표의 간격이 수위면의 정밀도를 결정하며,
수위면이 급변하는 구간에 대해서는 요소 절점 위치에 따라 세밀하게 간격을 설정해야
합니다.

특이
수압 함수
모델의
위치에 따른 상부와 하부의 수압을 정의합니다.
요소망
세트 수위를 지정할 때 정수 조건과 사용자 정의 조건에서 적용할 수 있습니다.
- 사용자
정의 조건 : 할당된 요소망의 상부와 하부의 수압을 사용자가 직접 특이 수압 함수를
이용하여 정의할 수 있습니다.
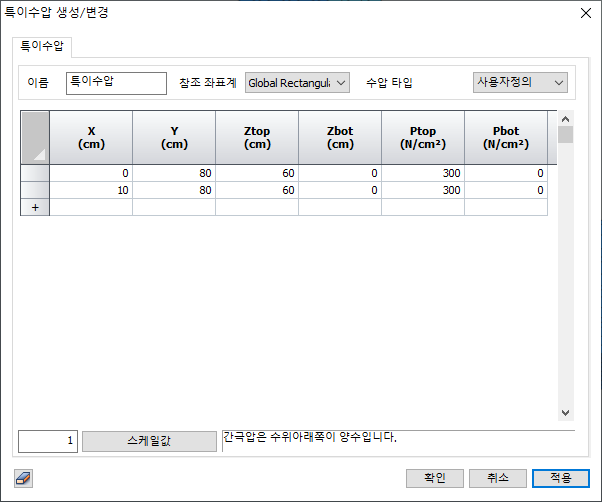
-
정수 조건 : 할당된 요소망의 최상부의 수압을 정수로 정의할 때 사용하는 기능입니다.
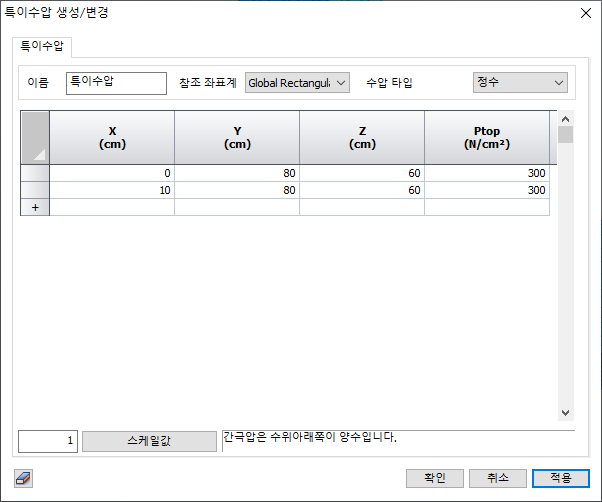
이름
– 기능 이름을 입력합니다.
Ref.
CSys – 기능 정의를 위한 참조 좌표계
수압식
– 분석 사례 > 분석 제어> 요소망 세트의 수위 정의 (사용자
정의 또는 정수 조건)애서 선택할 기능 유형을 선택합니다.
모든
입력 데이터를 증배하기 위한 배율 인수

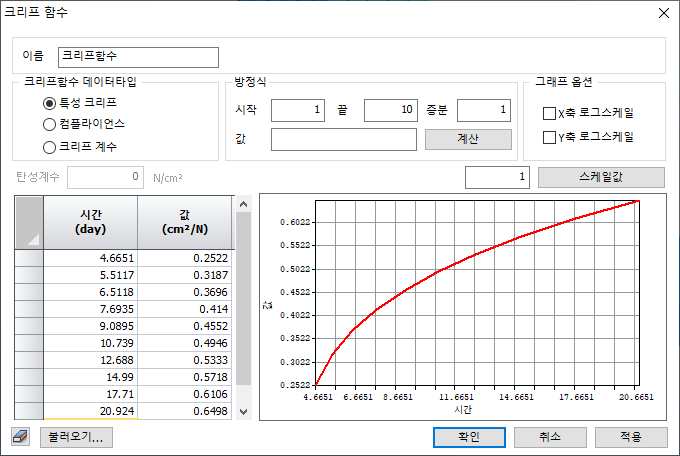
크리프 함수
시간에
따른 콘크리트의 크리프 특성을 정의합니다. 사용자 정의 코드일 때 크리프 함수를 직접
정의할 수 있습니다.
크리프 함수 데이터 유형에는 세 가지 유형이
있습니다.
특성
크리프 ; 즉시 처짐을
제외한 단위 응력 당 변형율
크리프
함수 ; 즉시 처짐을
포함한 단위 응력 당 변형율
크리프
계수 ; 탄성 변형율에
대한 크리프 변형율의 비
자주
사용하는 크리프 기능을 파일에 저장하고 불러올 수 있습니다. 파일형식 (fn.TDM)은
다음과 같습니다.
* Unit,
in, kip |
|
* Data |
적용할
단위를 지정 (선택 사항) |
20, 0.9934 |
'day'
and 'value'의 형식으로 Data 입력 (필수사항) |
40,1.2182 |
- |
60, 1.3705 |
- |
80,1.4883 |
- |
100, 1.5854 |
- |
120, 1.6683 |
- |
140, 1.7408 |
- |
160, 1.8054 |
- |
180, 1.8636 |
- |
200, 1.9166 |
- |
220, 1.9653 |
- |
240, 2.0103 |
- |
260, 2.0252 |
- |

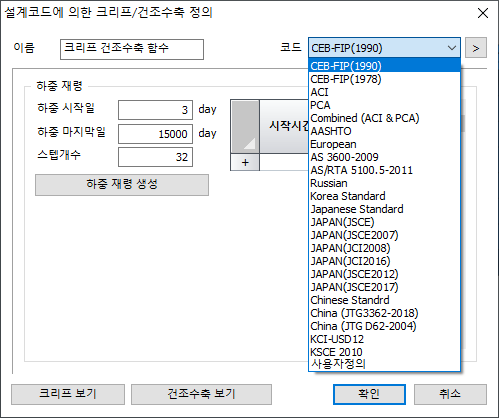
크리프/건조수축
함수 그룹
설계
코드에 의한 크리프/건조수축 기능 함수를 정의합니다.
Link to
Creep / Shrinkage Design Code

탄성 계수 함수
선택한
설계 코드를 기반으로 시간이 종속 탄성 계수 함수를 정의합니다. 단계 수와 함께 함수의
종료 시간을 입력해야 합니다.
Link to
Elastic Modulus Design Code

소성 경화 함수
등가 소성 변형율에 따른 경화 함수값을 직접
입력합니다. Modified Mohr coulomb
모델에서 전단 경화 거동을 정의할 때 사용됩니다. "자동 계산"
옵션을 사용하여 솔버는 편차 소성 변형을 기반으로 마찰 각도를 다시 계산합니다.

경화 곡선
Von Misese
재료 모델의 경화 곡선을 정의할 때 사용되는 함수입니다. 경화가 시작되면 나타나는
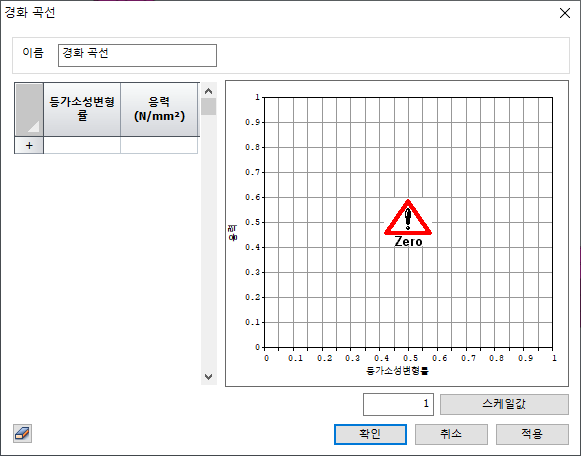
소성 변형은 아래의 식으로 표현할 수 있습니다.

응력 변형률 곡선
Von Misese
재료 모델의 응력-변형률 곡선을 정의할 때 사용되는 함수입니다. 하중-변위 곡선을
이미 알고 있는 경우, 실제 변형은 아래의 식으로 표현할 수 있습니다.
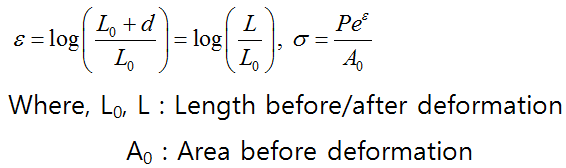

점착력 경화 곡선
소성 변형률 및
응집력을 직접 입력합니다.재료 모델의 점착력 경화 곡선을 정의할 때 사용되는 함수입니다.

마찰각 경화 곡선
소성 변형률 및
마찰각을 직접 입력합니다. CWFS (Cohesion Weakening and Frictional
Strengthening) 재료 모델의 마찰각 경화 곡선을 정의할 때 사용되는 함수입니다.

팽창각 경화 곡선
소성 변형률과
팽창각을 직접 입력합니다. CWFS (Cohesion Weakening and Frictional
Strengthening) 재료 모델의 팽창각 경화 곡선을 정의할 때 사용되는 함수입니다.

인장
강도 경화 곡선
소성 변형률과
인장 강도를 직접 입력합니다. CWFS (Cohesion Weakening and
Frictional Strengthening) 재료 모델의 인장 강도 경화 곡선을
정의할 때 사용되는 함수입니다.

침투 경계 시간 함수
절점 수두, 절점
(면) 유량 등 시간에 따른 수두, 유량 변화를 모사할 때 적용되는 함수입니다. 설정된
시간 단위에 맞게 시간 흐름에 따른 값 (수두/유량) 변화를 입력하여 함수를 생성하여
비정상류 침투 해석 수행 시 적용할 수 있습니다.
비정상류 침투 해석에서는 결과를 확인할 시간
스텝을 별도로 설정하며, 시간 스텝에 해당되는 시간의 함수값을 해석에 적용합니다.
여기서 시간 스텝이 함수의 시간 범위를 벗어나는 경우 범위 밖 보간에서 선형 보간
원칙에 따라 함수값을 자동 계산하여 적용합니다. 즉, 함수 범위를 벗어나는 시간 스텝에
대해 0의 함수값을 적용하고자 할 경우 함수 생성 시 위 그림의 예시와 같이 임의
시간 간격에 대해 동일한 함수값 (0)을 설정해 주어야 합니다.

비선형 탄성 함수 (트러스 요소)
트러스 요소 또는 임베디드 트러스 요소의
특성 정의 시 거동 특성을 비선형 탄성으로 정의할 수 있습니다. 이는 트러스 요소의
변형률에 대한 응력의 변화를 직접 함수로 생성하여 적용하는 방법입니다. 실제 적용하고자
하는 구조 부재 (트러스 계열)의 인장 (압축) 실험 결과를 이용하거나, 일반적인
강재의 변형 거동 특성을 입력할 수 있습니다.
.png)

비선형 탄성 함수 (점 스프링/탄성
링크 요소)
스프링, 탄성 링크와 같은 요소의 거동
특성을 비선형 탄성으로 정의할 수 있습니다. 요소 변형에 따른 스프링/링크의 강성을
정의하여 함수를 생성합니다.
.png)

불포화
특성 함수
침투 해석 중 지반을 포화 상태로 가정하는
정상류 해석의 경우 불포화 특성을 적용하여도 해석에 반영되지 않습니다. 반면에 시간에
따른 침투 결과를 검토하는 비정상류 해석에서는 지반의 불포화 특성을 반드시 고려해야
합니다. 또한, 실제 지반은 포화 상태보다는 대부분 일정 비율의 공기를 함유하고 있는
불포화 상태이기 때문에, 보다 현실적인 해석 결과 검토를 위해서는 불포화 특성이 고려된
비정상류 해석을 수행해야 합니다.
불포화 특성은 지반의 불포화 영역에서 음의
간극 수압 크기에 따른 투수 계수 및 함수비 (포화도) 변화를 정의하는 것으로 압력
수두(음의 간극 수압)에 따른 투수 함수와 함수비 함수를 직접 정의 (개별 고려)하는
방법과, 압력 수두-체적 함수비(포화도)-투수 계수비의 관계를 정의 (동시 고려)하는
방법이 있습니다.
[개별 정의]
투수
함수 데이터와 함수비 함수 데이터를 정의합니다. 불포화토 실험 데이터를 바탕으로 각각
제공되는 함수 종류에 따라 Curve Fitting을 통해 계수를 정의하거나, 사용자
정의를 통해 실험 데이터를 그대로 입력할 수 있습니다. 실험 데이터를 그대로 입력할
경우 음의 간극 수압 크기는 절대값으로 입력하고 투수 함수비는 포화 상태일 때 값으로
나눈 비율로 입력합니다.
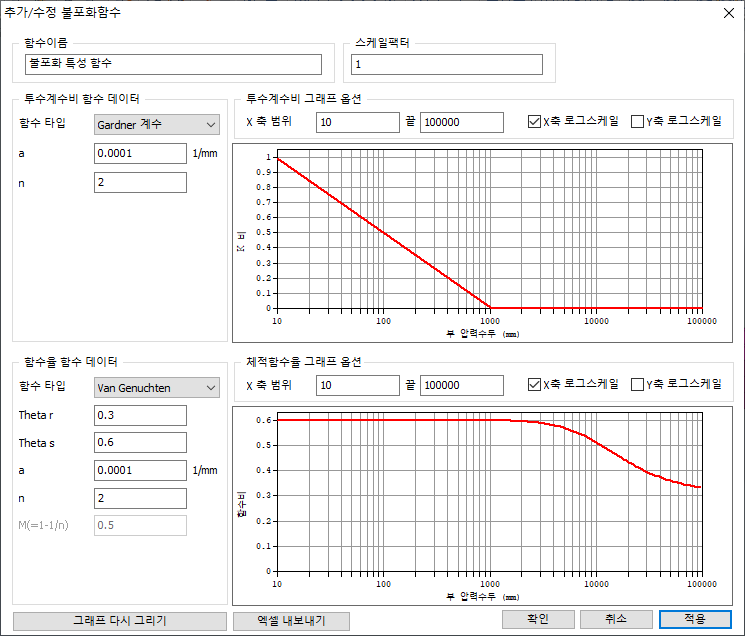
<Individual
consideration>
제공되는
투수 함수 종류 및 함수를 구성하는 계수의 의미는 아래와 같습니다.
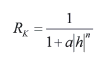
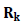 :
투수 계수비 (h의 증가에 따른 투수
계수 / h=0 일 때의 투수 계수) :
투수 계수비 (h의 증가에 따른 투수
계수 / h=0 일 때의 투수 계수)
a,
n : 불포화토 실험 데이터의 Curve Fitting을 통해 예측된 실험 상수
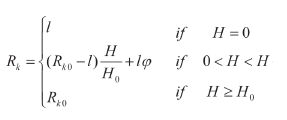
K ratio (Rk)
: 투수 계수비 (h의 증가에 따른 투수 계수 / h=0 일때의 투수 계수)
Ho
: 투수 계수가 더이상 감소하지 않을 때의 수두
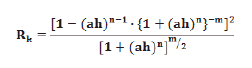
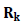 : 투수
계수비(h의 증가에 따른 투수 계수 / h=0 일 때의 투수 계수) : 투수
계수비(h의 증가에 따른 투수 계수 / h=0 일 때의 투수 계수)
a, n, m : 불포화토 실험 데이터의 Curve
Fitting을 통해 예측된 실험 상수
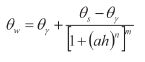
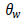 : 체적
함수비 : 체적
함수비
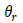 : 잔여
체적 함수비 : 잔여
체적 함수비
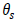 : 포화
체적 함수비 : 포화
체적 함수비
a, n, m : 불포화토 실험 데이터의 Curve Fitting을
통해 예측된 실험 상수

[관계 정의]
선택한 지반 종류에 따라 JICE (Japan
Institute of Construction Eng.) 기준의 불포화토 특성 재료
데이터를 설정할 수 있습니다. 지반 종류 별 제공되는 압력 수두-체적 함수율 (포화도)-투수
계수비 함수는 아래와 같습니다.
압력
수두 (P)-체적 함수율 (T)-비투수
계수 (K) |
압력 수두 (P)-포화도 (Sr)-비투수 계수 (K) |
(T)- (P) |
(T)-
(K) |
(Sr)-
(P) |
(Sr)- (K) |
역질토[G],[G-F],[GF]
(JICE) |
역질토
[G], [G-F],
[GF] (JICE) |
역질토
[G], [G-F], [GF] (JICE) |
역질토
[G], [G-F],
[GF] (JICE) |
사질토 [S], [S-F],
[SF] (JICE) |
사질토
[S], [S-F],
[SF] (JICE) |
사질토
[S],
[S-F], [SF] (JICE) |
사질토[S], [S-F],
[SF] (JICE) |
사질토
[SF] (JICE) |
점성토
[M], [C] (JICE) |
사질토l
[SF] (JICE) |
점성토l
[M], [C] (JICE) |
점성토 [M], [C] (JICE) |
사용자
정의 |
점성토
[M], [C] (JICE) |
사용자 정의 |
사용자
정의 |
|
사용자 정의 |
|
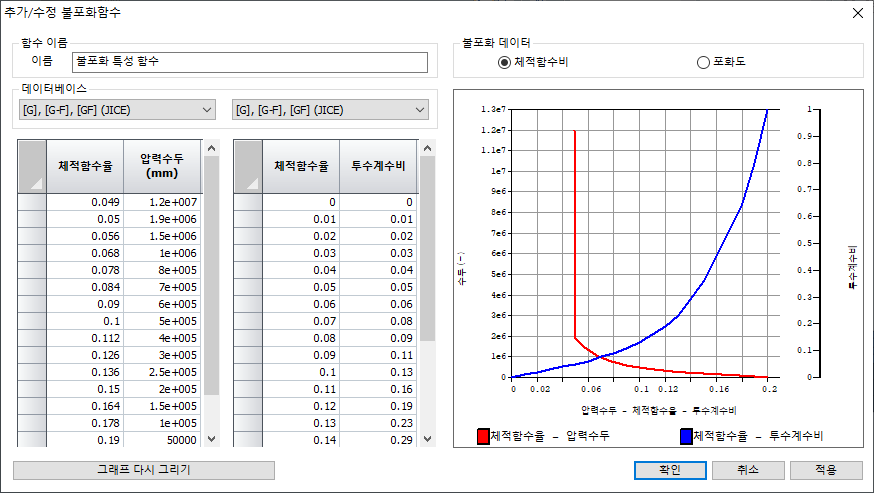
<동시 고려>
비정상류 해석에서는 시간 스텝 (시공
단계)마다 요소 절점 별로 음의 압력 수두 (음의 간극 수압)를 계산한 후 해당 스텝에
적용할 상대 투수 계수를 갱신합니다. 즉, 계산된 압력 수두로부터 압력 수두에 따른
체적 함수율 (포화도)를 구한 후 다시 체적 함수율 (포화도)에 따른 상대 투수 계수를
갱신하여 단계마다 적용합니다.

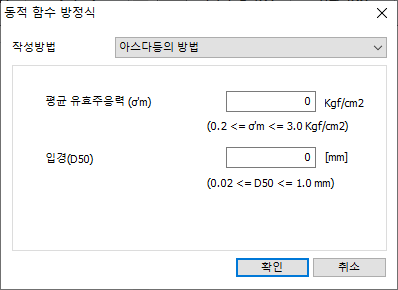
변형률 적합 특성 함수
2차원 등가 선형 해석 수행 시 지반의 비선형성과
비탄성 거동을 고려하기 위해 전단 탄성 계수와 감쇠비를 변형률에 따른 함수로 설정할
수 있습니다. 함수를 정의하지 않을 경우 지반 재료를 선형으로 가정하여 입력된 (고정된)
전단 탄성 계수와 감쇠비를 해석에 적용합니다. 일반적으로 지반은 전단 변형률이 증가함에
따라 전단 탄성 계수는 감소하고 감쇠비는 증가하는 경향을 보이는데, 복잡한 비선형
거동을 가지는 지반의 물성을 등가의 선형 거동을 하는 물성으로 단순화 하여 해석에
반영할 때 적용합니다. 가정된 초기값으로부터 반복 계산을 통해 수렴된 전단 탄성 계수
및 감쇠비를 산정할 수 있습니다.
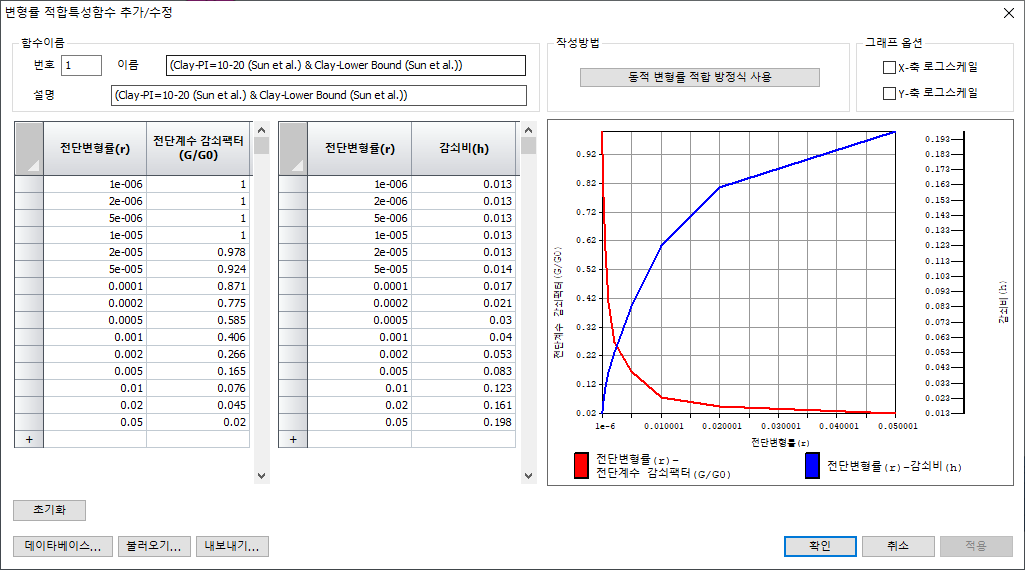
기존의 다양한 데이터 베이스로부터 물성값을
정의할 수 있습니다. 아래와 같은 관련 근거식을 이용하여 지층 특성에 따라 함수를
생성합니다.

[데이터
베이스]
기존 연구에 의해 축적된 데이터 베이스로부터
변형률 함수를 불러올 수 있으며, 아래와 같은 DB가 탑재되어 있습니다.
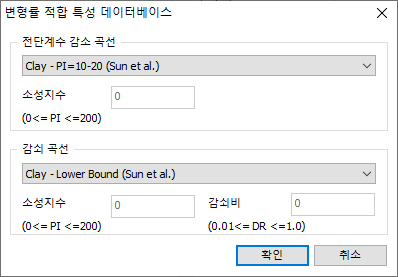
전단계수
감소
곡선 |
Clay
- Pl=5-10 (Sun et al.0) |
감쇠곡선 |
Clay
- Lower Bound (Sun et al.0) |
Clay
- Pl=10-20 (Sun et al.0) |
Clay - Average
(Sun et al.0) |
Clay - Pl=20-40
(Sun et al.0) |
Clay - Upper
Bound (Sun et al.0) |
Clay
- Pl=40-80 (Sun et al.0) |
Clay (Idriss
1990) |
Clay - Pl=80+
(Sun et al.0) |
Gravel (Seed
et al.0) |
Clay
(Seed and Sun 1989) |
Linear |
Gravel (Seed
et al.0) |
Rock |
Linear |
Rock (Idriss) |
Rock |
Sand (Idriss
1990) |
Rock
(Idriss) |
Sand (Seed
& Idriss) - Lower Bound |
Sand (Seed
& Idriss) - Lower Bound |
Sand (Seed
& Idriss) - Average |
Sand
(Seed & Idriss) - Average |
Sand (Seed
& Idriss) - Upper Bound |
Sand (Seed
& Idriss) - Upper Bound |
Vucetic
- Dobry |
Sand
(Seed and Idriss 1970) |
- |
Vucetic
- Dobry |

스펙트럼 함수
응답 스펙트럼 해석에 적용되는 스펙트럼 함수를
정의합니다. 응답 스펙트럼 해석에서는 구조물의 고유 주기에 해당하는 스펙트럼 함수
값을 선형 보간하여 사용하기 때문에 스펙트럼 곡선의 곡률이 급격히 변화하는 부분에
대해서는 여러 구간으로 나누어 조밀한 스펙트럼 값을 갖도록 하는 것이 바람직하고,
스펙트럼 함수의 주기 범위는 구조물의 고유 주기를 모두 포함하도록 하여야 합니다.
스펙트럼 데이터 종류는 정규화 가속도 (가속도
스펙트럼/중력 가속도), 가속도, 속도, 변위 스펙트럼이 있으며, 형식을 변경할 경우
데이터 형식의 단위에 따라 변환되지 않고 적용 형식만이 변경됩니다. 스케일 팩터는
입력된 데이터의 증감 계수이며, 최대값 설정으로 입력된 값이 최대가 되도록 전체 데이터를
스케일링 할 수 있습니다. .
‘감쇠비’ 란에는 Response Spectrum에
적용된 감쇠비를 입력하게 되는데 해석을 수행할 구조물의 감쇠비가 다를 경우에는 입력한
스펙트럼 데이터는 구조물 감쇠비에 맞게 가공하여 적용됩니다.
 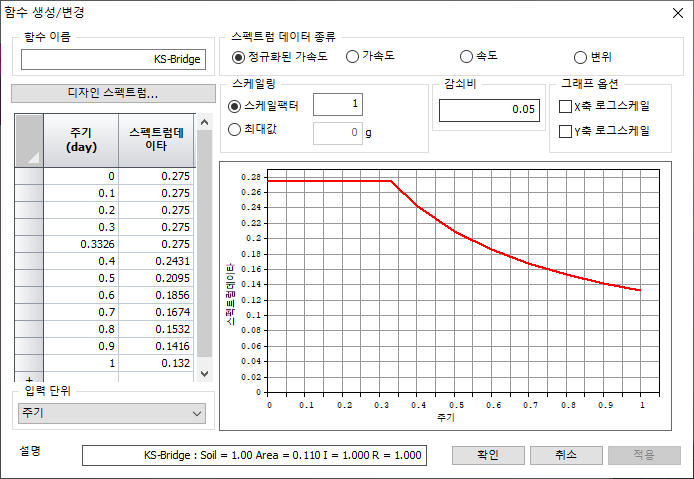
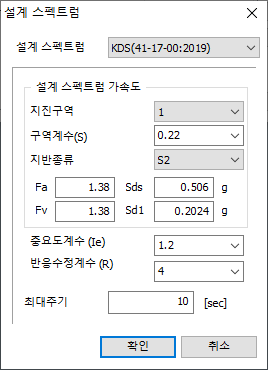
[디자인 스펙트럼 적용]
프로그램에
내장된 설계 스펙트럼을 이용할 수 있습니다. 기본적으로 내장되어 제공되는 설계용 스펙트럼
종류는 다음과 같습니다.
 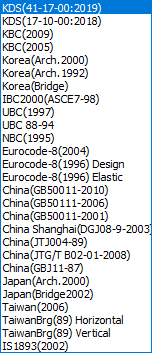
Korea
(Bridge) : 한국, 도로교 설계 기준 Japan
(Bridge02) : 일본, 건축물 하중 지침 및 동해석 China
(JTJ004-89) : 중국, 도로 공사 내진 설계 규준 KBC
2009 : 한국, 건축 구조 설계 기준 (2009) KBC
2005 : 한국, 건축 구조 설계 기준 (2005) IBC2000
(ASCE7-98) : 미국, International Building Code
2000 UBC
(1997) : 미국, UBC 97 규준 EURO (2004H-ELASTIC) : 유럽,
구조물의 내진 설계도

시간 이력 함수
선형/비선형
시간 이력 해석에 적용되는 하중 조건 (지반 가속도, 동적 절점(면) 하중에 적용되는
함수입니다. 시간에 따른 시간 이력 하중값을 구성하여 함수를 생성하며, 시간 함수
데이터 종류는 가속도, 힘 (하중), 모멘트, 정규화된 가속도 (시간 이력 가속도
/ 중력 가속도) 또는 일반 (정규화) 로 구분됩니다. 종류를 정할 경우 데이터 형식의
단위에 따라 변환되지 않고 적용 형식만이 변경됩니다. 스케일 팩터는 입력된 데이터의
증감 계수이며, 최대값을 설정하여 전체 데이터를 입력된 값으로 스케일링 할 수 있습니다.
[시간 함수 추가]
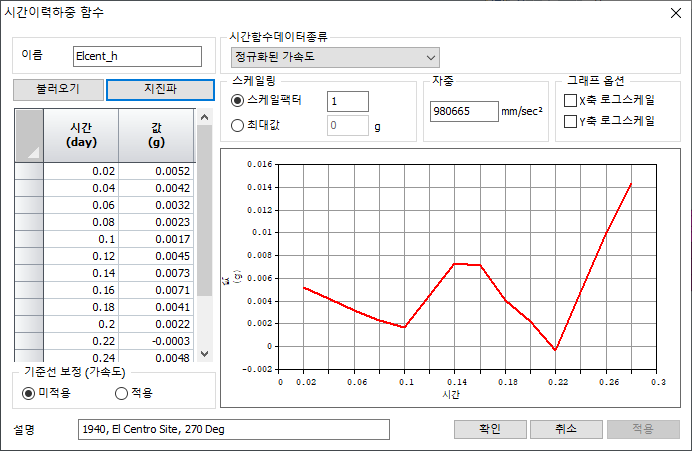
정의된 함수는 지반 가속도뿐 아니라,
동적 절점(면) 하중, 시간 변화 정적 하중 적용 시에도 사용됩니다. '힘' 또는
'모멘트'를 지정한 경우에는 시간 이력 하중을 "동적 절점 하중"으로
입력하는데 사용되고 '정규화 가속도' 또는 '가속도'를 지정한 경우에는 지반 가속도
기능에서 "지반 가속도" 등을 입력하는데 사용됩니다. '일반'을
지정한 경우에는 시간 이력 하중이 "시간 변화 정적 하중", 또는
"동적 면하중" 기능에서 정적하중의 시간에 따른 변화를 입력하는데
사용됩니다.
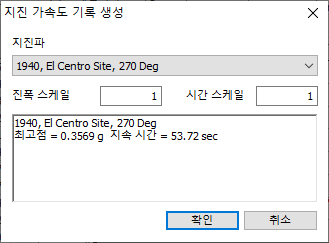
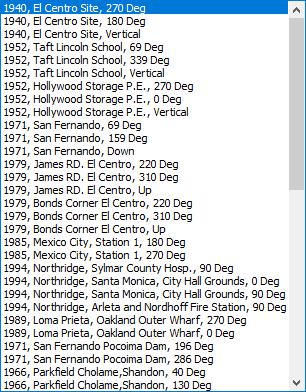
[불러오기/지진파]
자주 사용하는 시간 이력 하중을 파일로
저장하여 불러오거나, 프로그램에 내장된 DB로 부터 지진 가속도를 선택할 수 있습니다.
총 32종의 지진 가속도가 내장되어 있습니다.

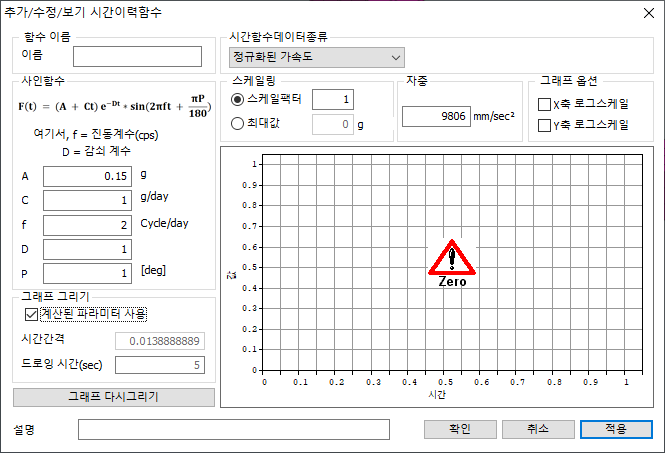
[사인 함수 추가]
사인 함수를 이용하여 시간 이력 하중을
정의할 수 있습니다. A,C 는 상수, f는 입력 하중의 진동수 (Frequency),
D는 감쇠 계수 (Damping Factor), P는 위상각을 의미합니다. 조화 함수
형태로 시간 이력 하중를 입력하고자 할 경우에는 사인함수에 필요한 변수를 입력하고,
그래프 다시 그리기를 클릭하면 오른쪽에 이력 하중이 그래프 형태로 나타납니다.

|


![]()