Hyperbolic 모델의 주요
비선형 파라미터는 아래와 같습니다.
/06._Hyperbolic(Duncan-Chang)_E_v.png) /07._Hyperbolic(Duncan-Chang)_E_B.png)
Hyperbolic
(Duncan-Chang E-v) Hyperbolic
(Duncan-Chang E-B)
마찰각
증가는 거친 입자의 토양으로부터 구속 압력이 증가하는 동안 마찰각이 감소하는 것을 설명할 수 있습니다.
마찰각 증분은 다음 식으로 정의됩니다.
/Duncan_Chang/4.png)
마찰
각도 증분 값은 0보다 커야 합니다.
실험
변수 값 (G, F 및 D)은 쌍곡선 (Duncan-Chang E-v)에서 프아송 비 매개변수를
계산하기 위해 추가됩니다. G는 초기 프아송 비로부터 축까지의 거리, F는 초기 프아송 비로부터
압축에 대한 변화율, D는 초기 프아송 비로부터 응력에 대한 변화율이다.
그
값의 한계와 다음 방정식으로 정의되는 프아송 비 매개변수.
/Duncan_Chang/3.png)
삼축
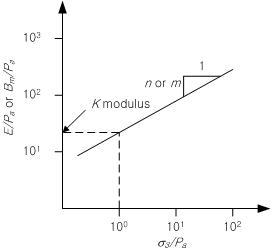
압축 시험 결과로부터 아래 그림과 같이 세로 축이 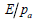 또는 또는 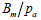 가
되도록 하고 가로 축을 가
되도록 하고 가로 축을 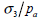 이 되도록 그래프를 그릴 수 있습니다.
각 축을 log 스케일로 맞춘 후, 이 되도록 그래프를 그릴 수 있습니다.
각 축을 log 스케일로 맞춘 후, 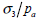 =1 인 점에서의 세로
축 값이 초기 재하 계수 (K)가
됩니다. 세로 축이 =1 인 점에서의 세로
축 값이 초기 재하 계수 (K)가
됩니다. 세로 축이 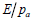 일 때 그래프 기울기로부터 초기 강성 지수 (n)을
구할 수 있으며, 일 때 그래프 기울기로부터 초기 강성 지수 (n)을
구할 수 있으며, 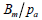 일 때 그래프 기울기로부터 부피 계수 지수(m)을
구할 수 있습니다. 여기서 부피 계수 Bm 은 아래 식과 같이 정의되며, 프아송 비와의 관계로부터
예측할 수 도 있습니다. 여기서 프아송 비는 0 에서 0.5 이하의 값으로 제한합니다. 일 때 그래프 기울기로부터 부피 계수 지수(m)을
구할 수 있습니다. 여기서 부피 계수 Bm 은 아래 식과 같이 정의되며, 프아송 비와의 관계로부터
예측할 수 도 있습니다. 여기서 프아송 비는 0 에서 0.5 이하의 값으로 제한합니다.
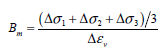
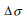 : 주응력의 변화량, : 주응력의 변화량,
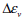 : 부피 변형률의 변화량 : 부피 변형률의 변화량

<재료
물성 결정>

Duncan
and Chang의 비선형 응력-변형률 곡선은 응력 상태와 응력 경로에 따라 세 가지 지반 계수
(초기 계수 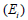 ,
접선 계수 ,
접선 계수 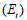 ,
제하-재재하 (unloading-reloading)계수 ,
제하-재재하 (unloading-reloading)계수 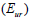 )로 정의됩니다. )로 정의됩니다.
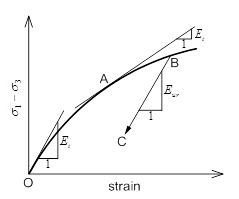
<비선형
응력-변형률 거동>
여기서,
초기 계수 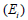 와
접선 계수 와
접선 계수 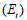 의
관계에서 파괴비 (Rf)를
구할 수 있습니다. 파괴비는 쌍곡선에 대한 점근선과 최대 전단 강도 비로 일반적으로 0.75~1
사이 값을 갖습니다. 접선 계수 의
관계에서 파괴비 (Rf)를
구할 수 있습니다. 파괴비는 쌍곡선에 대한 점근선과 최대 전단 강도 비로 일반적으로 0.75~1
사이 값을 갖습니다. 접선 계수 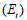 는 값이 너무 작을 경우 수렴
문제를 야기할 수 있기 때문에 최소 접선 계수의 기본값은 대기압 (Pa) 입니다. 는 값이 너무 작을 경우 수렴
문제를 야기할 수 있기 때문에 최소 접선 계수의 기본값은 대기압 (Pa) 입니다.
부피 계수 번호 (Kb)는 부피 계수
(Bm)과 부피 계수 지수 (m)으로부터 계산됩니다.

여기서,
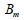 : 부피 계수 (bulk modulus), : 부피 계수 (bulk modulus),
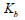 : 부피 계수 번호 : 부피 계수 번호
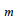 : 부피
계수 지수 : 부피
계수 지수
제하-재재하 계수 번호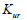 은 제하-재재하 계수 은 제하-재재하 계수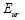 로 부터 계산됩니다. 로 부터 계산됩니다.

초기
계수를 구할 때 적용되는 구속 응력은 '0 (zero)' 이거나 음수 (인장 상태)가 될 경우 초기
계수가 '0 (zero)' 이나 음수가 될 수 있으므로 구속 응력에 대한 하한치 설정이 필요하며,
설정된 최소 구속 압력 은
0.01Pa 입니다.
사질토의
밀도에 따른 파라미터 제안값은 아래와 같습니다. (Duncan, J. M. and Chan, C.
Y. (1970))
Relative
density |
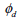
|
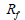
|
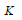
|
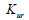
|

|
100%
(dense) |
36.5 |
0.91 |
2000 |
2120 |
0.54 |
38%
(loose) |
30.4 |
0.90 |
295 |
1090 |
0.65 |
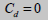 for
dense and loose sand for
dense and loose sand
|
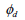 , ,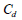 :
건조 상태에서 마찰각과 점착력 :
건조 상태에서 마찰각과 점착력
<표. Summary of stress-strain
parameters for uniform fine silica sand>
|


![]()