1차원
요소
기하
특성으로 길이를 가지며, 2개 (1차) 또는 3개 (2차)의 절점으로 구성되는 요소입니다. 3차원
형상을 1차원 요소로 표현하기 때문에 단면 (크기, 형상)을 정의해야 하고, 이를 이용해서 2차원
요소로 모델링한 후 계산됩니다.
FEA
NX에서는 아래 그림과 같이 다양한 형상을 제공하고 있습니다. 단면 특성 정의 시 Offset 위치를
추가 설정할 수 있습니다.

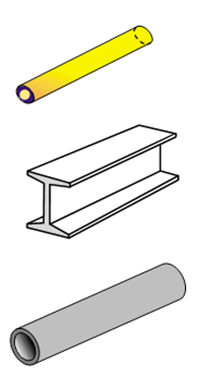 
<실제 모델> <유한요소
모델>

QUAD-4 6400개
<Solid
square> |

QUAD-4 3400개
<H section> |

QUAD-4 1700개
<Channel> |
<단면 자동 모델링 >
<Solid
Rectangle>
|
<Solid
Round>
|
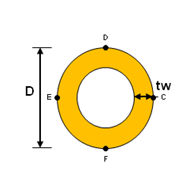
<Pipe>
|
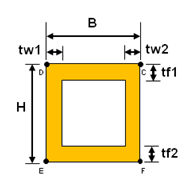
<Box>
|
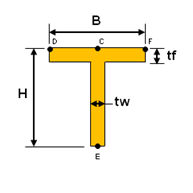
<T-section>
|
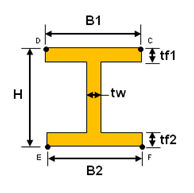
<H-section>
|
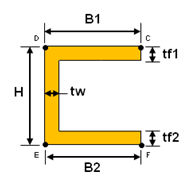
<Channel>
|
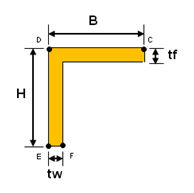
<Angle>
|
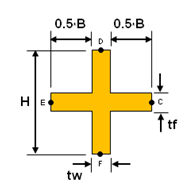
<Cross>
|
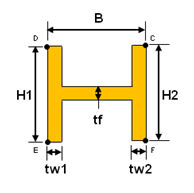
<I-section>
|
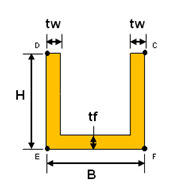
<Channel
1>
|
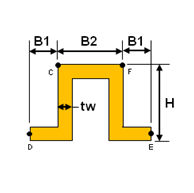
<Hat>
|
<단면 형상 및 치수 정의>

2차원 요소
기하
특성으로 면적을 가지는 삼각형 (Triangle) 또는 사각형 (Quadrilateral) 입니다.
3차원 형상을 2차원 요소로 표현하기 때문에 두께를 정의해야 합니다. 두께는 동일 또는 위치 별
변단면을 설정할 수 있습니다.

<실제 모델> <유한요소
모델>

3차원 요소
기하
특성으로 체적을 가지는 사면체 (Tetrahedron) 또는 육면체 (Hexahedron, Brick)
형상의 요소입니다.
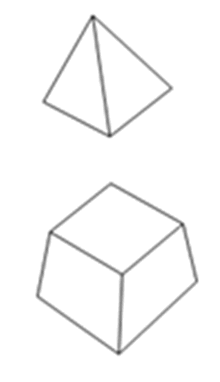 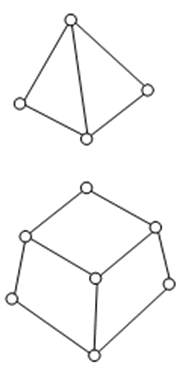
<실제 모델> <유한요소
모델>
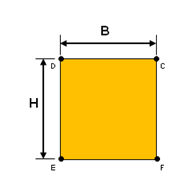
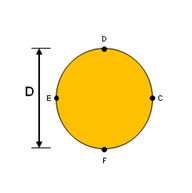
단면적 (A)
단면적
(cross sectional area)은 부재가 인장 또는 압축력 (axial force)을 받는
경우 이에 저항하는 축강성 (axial stiffness)을 계산하거나 부재에 발생한 응력을 계산하는데
사용되며, 계산 방법은 H형 단면에 대해서 그림과 같습니다.
FEA
NX 내부에서 단면적을 계산하는 방법은 두 가지가 있습니다. 첫 번째 방법은 제공되는 단면 형상에
대한 데이터 베이스로부터 요구되는 단면의 치수를 입력하여 자동으로 단면적을 계산하는 방법이며, 두
번째 방법은 사용자가 직접 단면적을 계산하여 입력하는 방법이 있습니다. 첫 번째 방법은 사용 상에
편리하다는 장점이 있으나, 실제 단면 형상에서 발생되는 접합부의 볼트, 접합 구멍 및 리벳 접합
구멍 등에 의한 단면적의 감소 요인은 고려하지 않으므로, 사용자가 직접 계산된 단면적을 입력하는
두 번째 방법이 더 정확한 결과를 나타낼 수 있습니다.
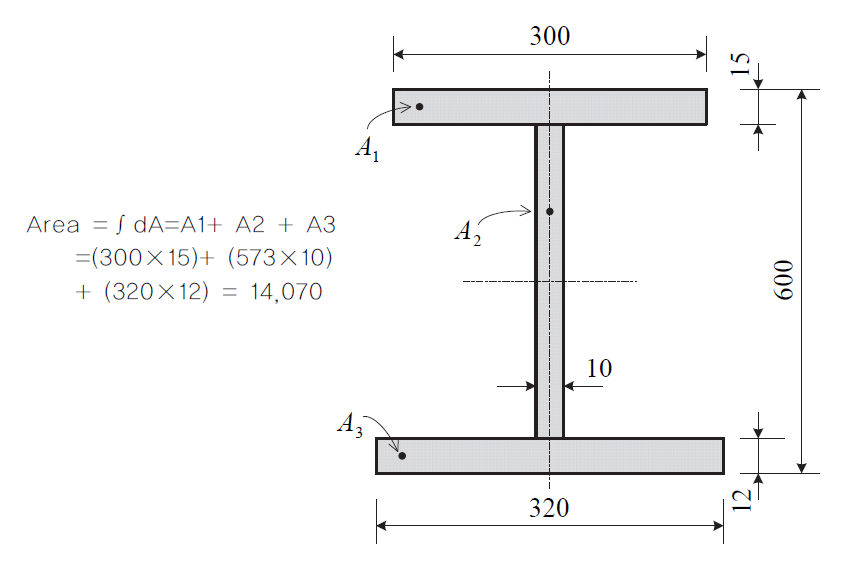
<단면적의 계산 예>

비틀림 강성 (Ixx)
비틀림
강성은 비틀림 모멘트에 저항하는 강성으로 다음과 같이 표현됩니다.
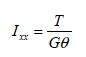
여기서,
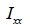 : 비틀림 강성 (torsional resistance), : 비틀림 강성 (torsional resistance),
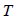 : 비틀림 모멘트
(Torsional moment or torque), : 비틀림 모멘트
(Torsional moment or torque),
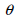 : 비틀림 각도 (angle
of twist), : 비틀림 각도 (angle
of twist),
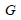 : 전단 탄성 계수 : 전단 탄성 계수
비틀림
강성은 위 식에서와 같이 비틀림에 저항하는 강성이며, 비틀림에 의한 전단 응력을 결정하는 극관성
단면 2차모멘트 (polar moment of inertia)와는 다릅니다
(단,
원형 단면 또는 두께가 두꺼운 원통 단면의 경우는 비틀림 모멘트와 극관성 단면 2차 모멘트가 일치합니다.).
비틀림
강성의 경우 와 Saint-venant의 비틀림 이론을 이용하여 아래와 같이 계산됩니다.
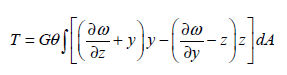
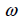 는 함수로 (warping function) 는 함수로 (warping function) 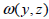 의 함수이며, 유한 요소법으로 아래의 방정식을 이용하여 계산합니다.
의 함수이며, 유한 요소법으로 아래의 방정식을 이용하여 계산합니다.
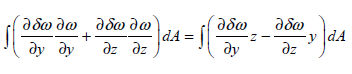
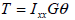 이므로, 비틀림 강성 성분은 다음과 같이 나타낼수 있습니다. 이므로, 비틀림 강성 성분은 다음과 같이 나타낼수 있습니다.
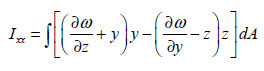

유효 전단면적 (Asy, Asz )
전단력에
대한 유효 전단면적 (effective shear area)은 부재 단면의 요소 좌표계 y축 또는
z축 방향으로 작용하는 전단력 (shear force)에 저항하는 강성 (shear stiffness)의
계산에 필요합니다. 만약, 유효 전단면적을 입력하지 않았을 경우에는 해당 방향의 전단 변형이 무시됩니다.
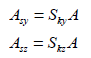
여기서,
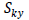 : 요소 좌표계 y축
방향으로 작용하는 전단력에 저항하는 유효 전단 계수 : 요소 좌표계 y축
방향으로 작용하는 전단력에 저항하는 유효 전단 계수
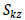 : 요소 좌표계 z축
방향으로 작용하는 전단력에 저항하는 유효 전단 계수 : 요소 좌표계 z축
방향으로 작용하는 전단력에 저항하는 유효 전단 계수
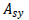 : 요소 좌표계 y축 방향으로 작용하는
전단력에 저항하는 유효 전단면적 : 요소 좌표계 y축 방향으로 작용하는
전단력에 저항하는 유효 전단면적
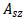 : 요소 좌표계 z축 방향으로 작용하는
전단력에 저항하는 유효 전단면적 : 요소 좌표계 z축 방향으로 작용하는
전단력에 저항하는 유효 전단면적
내부에서
단면 물성을 계산하거나 데이터 베이스로부터 입력되는 경우에는 해당 전단 강성 성분이 자동 고려되며,
유효 전단 계수의 계산 방법은 휨모멘트로 발생된 전단력에 의한 뒴 함수(warping function)
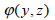 와
Saint-venant의 비틀림 이론의 뒴 함수 와
Saint-venant의 비틀림 이론의 뒴 함수 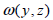 를 이용하여 아래와
같이 계산됩니다. 를 이용하여 아래와
같이 계산됩니다.
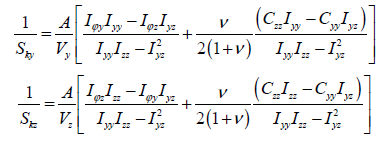
여기서,
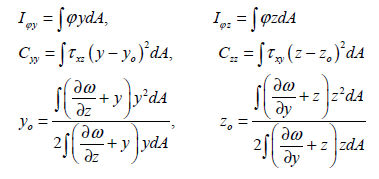

단면 2차 모멘트 (Iyy, Izz)
단면
2차 모멘트 (area moment of inertia)는 휨 모멘트 (bending moment)에
저항하는 휨 강성 (flexural stiffness)을 계산하는데 사용되며, 해당 단면의 도심축에서
다음의 식에 따라 계산됩니다.
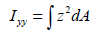
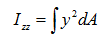
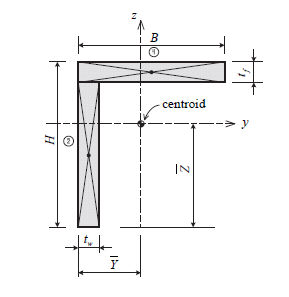
Section element |
b |
h |
|
|
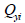
|
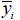
|
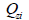
|
① |
10 |
4 |
40 |
2 |
80 |
5 |
200 |
② |
2 |
10 |
20 |
9 |
180 |
5 |
100 |
③ |
8 |
3 |
24 |
15.5 |
372 |
5 |
120 |
total |
- |
- |
84 |
- |
632 |
- |
420 |
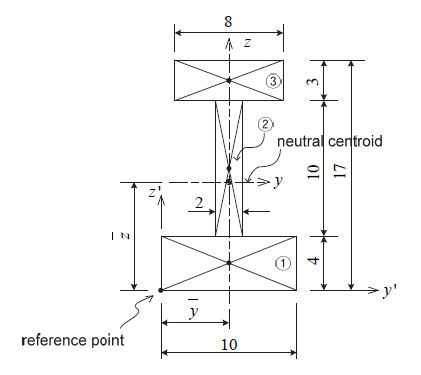
<표. 단면 1차 모멘트 및 도심의 계산>
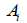 : 단면적 : 단면적
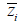 : 기준점에서 z ' 축 방향으로 단면 요소의 중심까지의
거리 : 기준점에서 z ' 축 방향으로 단면 요소의 중심까지의
거리
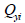 : 기준점에 대한 y ' 축 방향의 1차 모멘트 : 기준점에 대한 y ' 축 방향의 1차 모멘트
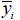 : 기준점에서
y ' 축 방향으로 단면 요소의 중심까지의 거리 : 기준점에서
y ' 축 방향으로 단면 요소의 중심까지의 거리
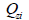 : 기준점에 대한 z
' 축 방향의 1차 모멘트 : 기준점에 대한 z
' 축 방향의 1차 모멘트
중립축 위치 계산 ( 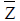 , , 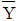 ) )
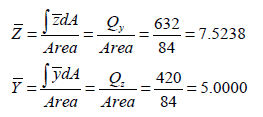
단면 2차 모멘트 계산 ( 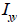 , , 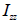 ) )
Section element |
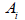
|
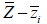
|
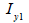
|
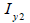
|
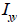
|
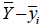
|
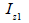
|
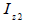
|
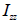
|
① |
40 |
5.5328 |
1224.5 |
53.3 |
1277.8 |
0 |
0 |
333.3 |
333.3 |
② |
20 |
1.4672 |
43.1 |
166.7 |
209.8 |
0 |
0 |
6.7 |
6.7 |
③ |
24 |
7.9762 |
1526.9 |
18.0 |
1544.9 |
0 |
0 |
128.0 |
128.0 |
total |
|
2794.5 |
238.0 |
3032.5 |
|
0 |
468.0 |
468.0 |
|
<표. 단면 2차 모멘트의 계산 예>
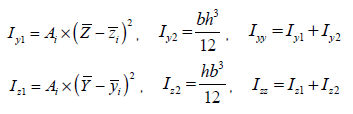

단면 상승 모멘트 (Iyz)
단면
상승 모멘트 (area product moment of inertia)는 비대칭 단면의 응력 성분을
계산하는데 사용되며, 그 정의는 다음과 같습니다.
H,
pipe, box, channel, tee형 단면과 같이 요소 좌표계 y, z축 어느 1개의 축에
대해서 대칭인 경우에는 Iyz=0이 되며, angle 형 단면과 같이 어느 1개 축에 대해서도 대칭이
아닌 경우에는 Iyz≠ 0이므로 응력 성분 계산 시 고려하여야 합니다.
angle
형 단면의 단면 상승 모멘트 계산 방법은 아래 그림과 같습니다.
 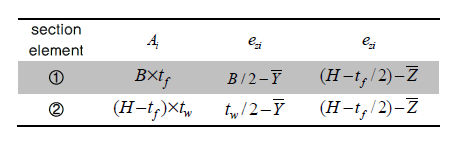
<angle 형 단면의 단면 상승 모멘트 계산>
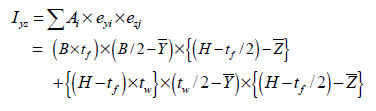
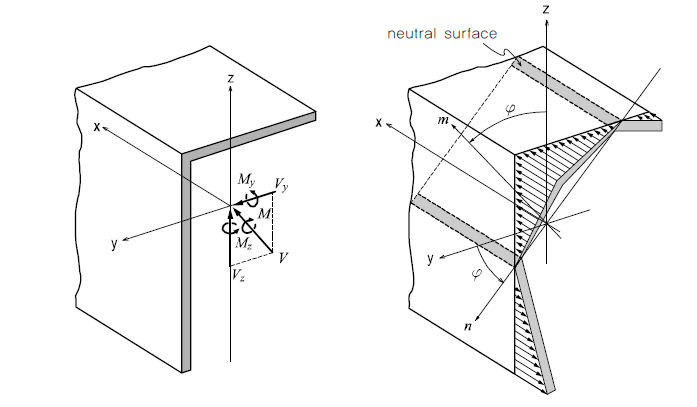
< 비대칭형 단면에서의 휨응력 분포도>
중립축
(neutral axis)은 휨모멘트에 의한 부재 내 휨응력이 ‘0 (zero)’이 되는 위치를
통과하는 축을 말하며, n-축이 중립축이 됩니다. m-축은 n-축에 대하여 수직을 이루는 축입니다.
중립축에서는
휨모멘트에 의한 휨응력이 ‘0’이므로 다음의 관계식으로부터 중립축 방향을 구할 수 있습니다.
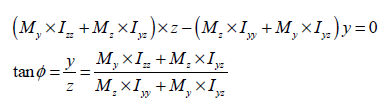
휨모멘트에
의한 단면의 휨응력을 계산하는데 적용되는 일반식은 다음과 같습니다.
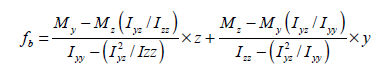
만약
H형 단면일 경우에는 , 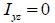 이 되므로, 이 되므로,
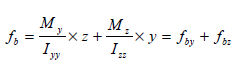
여기서,
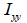 : 요소 좌표계 축에 대한 단면 2차
모멘트, : 요소 좌표계 축에 대한 단면 2차
모멘트,
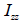 : 요소 좌표계 축에 대한 단면 2차 모멘트, : 요소 좌표계 축에 대한 단면 2차 모멘트,
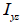 : 단면 상승 모멘트, : 단면 상승 모멘트,
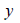 : 요소 단면의 중립축으로부터 휨응력을
계산하고자 하는 위치까지의 요소 좌표계 축 방향의 거리, : 요소 단면의 중립축으로부터 휨응력을
계산하고자 하는 위치까지의 요소 좌표계 축 방향의 거리,
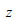 : 요소 단면의 중립축으로부터 휨응력을
계산하고자 하는 위치까지의 요소 좌표계 축 방향의 거리, : 요소 단면의 중립축으로부터 휨응력을
계산하고자 하는 위치까지의 요소 좌표계 축 방향의 거리,
 : 요소 좌표계 축에 대한 휨모멘트, : 요소 좌표계 축에 대한 휨모멘트,
 : 요소 좌표계 축에 대한 휨모멘트 : 요소 좌표계 축에 대한 휨모멘트
요소
좌표계 y축 및 z축 방향으로 작용하는 전단력에 대한 전단 응력을 계산하는데 적용되는 일반식은 다음과
같습니다.
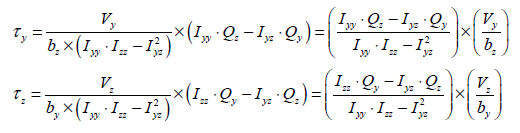
여기서,
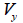 : 요소 좌표계 축 방향으로 작용하는 전단력, : 요소 좌표계 축 방향으로 작용하는 전단력,
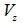 : 요소 좌표계 축 방향으로 작용하는 전단력, : 요소 좌표계 축 방향으로 작용하는 전단력,
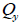 : 요소 좌표계 축에 대한 단면 1차 모멘트, : 요소 좌표계 축에 대한 단면 1차 모멘트,
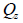 : 요소 좌표계 축에 대한 단면 1차 모멘트, : 요소 좌표계 축에 대한 단면 1차 모멘트,
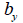 : 전단 응력을 계산하고자 하는 위치에서의 요소 좌표계
축과 직각을 이루는 단면의 두께, : 전단 응력을 계산하고자 하는 위치에서의 요소 좌표계
축과 직각을 이루는 단면의 두께,
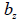 : 전단 응력을 계산하고자 하는 위치에서의 요소 좌표계
축과 직각을 이루는 단면의 두께 : 전단 응력을 계산하고자 하는 위치에서의 요소 좌표계
축과 직각을 이루는 단면의 두께

단면 1차 모멘트 (Qy, Qz)
단면
1차 모멘트 (first moment of area)는 단면의 임의의 위치에서 전단 응력을 계산하는데
사용되며 아래와 같이 계산합니다.
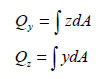
단면이
y, z 양축 중에서 어느 한 축에 대하여 대칭일 경우, 임의의 위치에서 전단 응력은 다음과 같이
계산합니다.
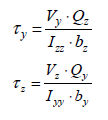
여기서,
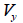 : 요소 좌표계 y축 방향으로 작용하는 전단력, : 요소 좌표계 y축 방향으로 작용하는 전단력,
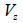 : 요소 좌표계 z축 방향으로 작용하는 전단력, : 요소 좌표계 z축 방향으로 작용하는 전단력,
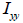 : 요소 좌표계 y축에 대한 단면 2차 모멘트, : 요소 좌표계 y축에 대한 단면 2차 모멘트,
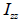 : 요소 좌표계 z축에 대한 단면 2차 모멘트, : 요소 좌표계 z축에 대한 단면 2차 모멘트,
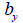 : 전단 응력을 계산하고자 하는 위치에서의 요소 좌표계
y축돠 직각을 이루는 단면의 두께, : 전단 응력을 계산하고자 하는 위치에서의 요소 좌표계
y축돠 직각을 이루는 단면의 두께,
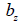 : 전단 응력을 계산하고자 하는 위치에서의 요소 좌표계
z축과 직각을 이루는 단면의 두께 : 전단 응력을 계산하고자 하는 위치에서의 요소 좌표계
z축과 직각을 이루는 단면의 두께
요소 두께
FEA
NX에서는 평면 응력 요소, 2D 토목 섬유 요소, 판 요소, 평면 변형 요소, 축대칭 요소, 선형
계면 요소 등을 정의하기 위해 요소의 두께를 정의하여야 합니다. 이중에서 평면 변형 요소와 축대칭
요소 및 선형 계면 요소의 경우는 내부적으로 단위 두께인 1을 사용하고 있습니다.
평면
응력 요소, 2D 토목 섬유 요소, 판 요소의 경우는 사용자가 직접 입력한 두께 값을 사용합니다.
이때 판 요소의 경우 회전 자유도를 가지고 있고, 이에 대한 비선형 해석이 가능하기 때문에 두께
방향으로 별도의 적분이 수행되어야 합니다.
간격
이
기능은 2D 프로젝트 설정에서만 활성화되는 1D 요소 속성에 있습니다. 이 옵션은 2D 모델에서
수평 방향 (두께 방향) 축을 따라 1D 요소를 도입할 때 각 요소 당 1D 요소의 힘을 고려하기
위해 사용됩니다.
FEA
NX에서 사용자가 간격 옵션을 선택 취소하면 해설 설정에서 평면 변형률 두께로 간주됩니다. 즉,
선택한 단위 시스템을 기반으로 하는 단위 두께를 의미합니다.
 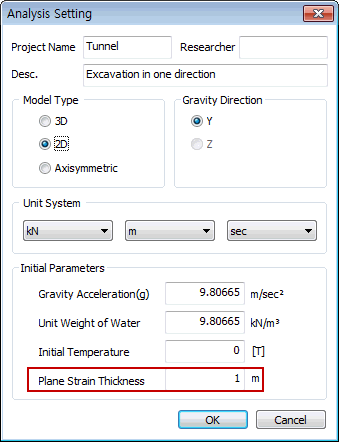
FEA
NX에서, 간격은 요소의 강성을 계산하고 각 요소 별 부재력을 출력하는데 사용됩니다.
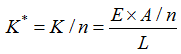
여기서,
n =간격, L = 길이 , A = 면적, K* = 간격을 고려한 강성
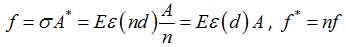
where,
f* = 부재력
아래의
예시를 참고합니다.
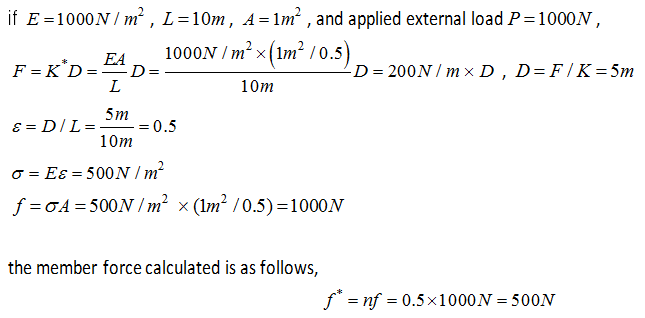
|


![]()