Time History Load Cases
▒ 기능
1. Masses 메뉴에서 제공하는 각종 질량 입력기능을 이용하여 모델에 질량데이터를 입력합니다. 2. Analysis>Eigenvalue Analysis Control 메뉴를 호출하여 해석할 고유모드수와 고유치해석에 필요한 각종 데이터를 입력합니다. 3. Load>Time History Analysis
Data>Time Forcing
Functions 기능을 선택하여 4. Load>Time History Analysis Data>Time History Load Cases 기능을 이용하여 load case name을 입력하고, 시간이력해석과정과 출력과정에 필요한 데이터, 그리고 damping ratio 등을 입력합니다. 5. Time Forcing Function을 지반운동으로 입력할 경우 : Load>Time History Analysis Data>Ground Acceleration 기능 이용하여 Time History Load Case Name과 각 방향별 Function Name 및 Angle of Horizontal Ground Acc.등을 입력합니다. Time Forcing Function을 동적절점하중으로 입력할 경우 : Load>Time History Analysis Data>Dynamic Nodal Loads 기능을 이용하여 하중을 적용할 Time History Load Case Name과 Function Name을 선택하고 하중방향, Arrival Time 등을 입력합니다. Time Forcing Function을 정적하중재하율로 입력할 경우 : Load>Time History Analysis Data>Time Varying Static Loads 기능을 이용하여 하중을 적용할 Time History Load Case Name과 Static Load 및 Function Name을 선택하고 하중방향, Arrival Time 등을 입력합니다. 6. Analysis>Perform
Analysis 메뉴와 7. 해석이 성공적으로 완료되면 Results 메뉴의 각종
후처리기능을 이용하여 해석결과를 정적해석결과와 조합하거나 분석합니다. 모든 해석결과는 주어진 시간이력동안의 최대값, 최소값, 최대절대값으로 출력되며, 각 시각별 거동 결과를 분석할 때는 Results>Time History Results 기능을 이용하여 시간이력그래프와 text형식의 출력물을 작성합니다. |
시간이력해석조건과
시간이력해석의 수행에 필요한 각종 제어용 데이터를 입력합니다.
버튼을 누른 다음, 대화상자에서 
▒ 호출
|
▒ 입력
 |
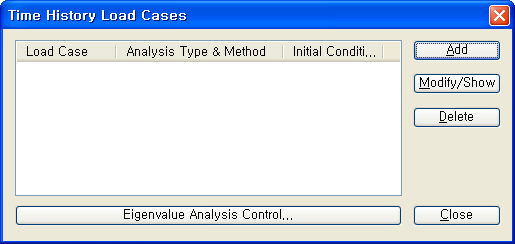: 고유치해석 정보를 입력합니다. |
: 시간이력해석 조건을 신규로 입력하거나 추가합니다.
: 입력된 시간이력해석 조건을 수정하거나 입력된 시간이력해석 조건을 확인합니다.
: 입력된 시간이력해석 조건을 삭제합니다.
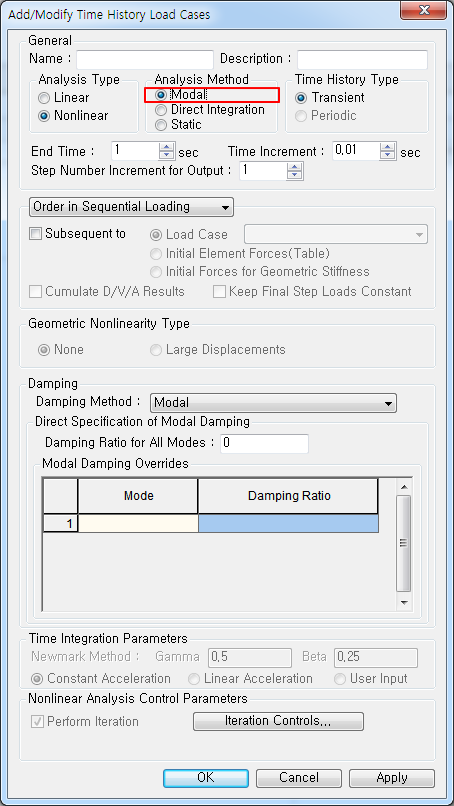
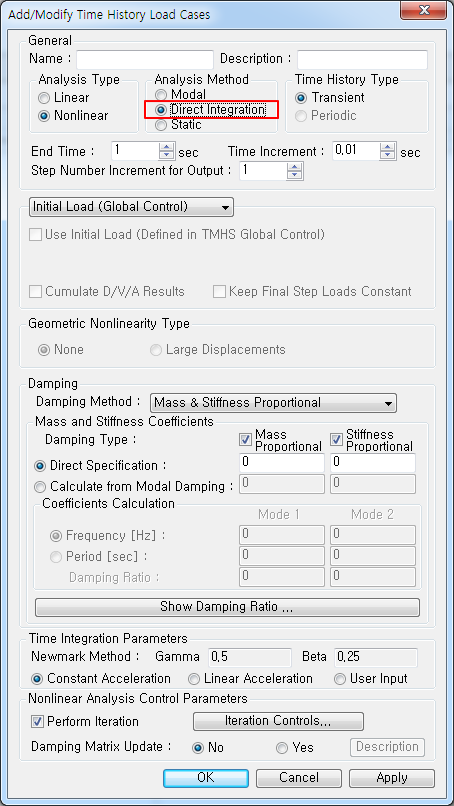
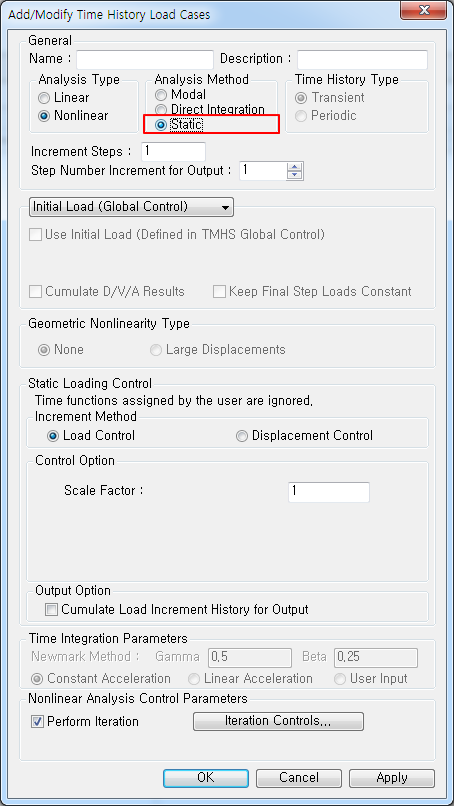
Add/Modify Time History Load Cases 대화상자
General |
시간이력해석조건의 명칭을 입력합니다. 이 명칭은 Combinations 기능에서 하중조합시 사용됩니다.
간단한 설명문을 입력합니다.
Linear : 선형 시간이력해석 Nonlinear : 비선형 시간이력해석
Modal : 모드중첩법 구조해석 프로그램에서 가장 많이 사용되는 것으로 대형구조물의 선형 동적해석에 매우 효과적인 방법입니다. 그러나 비선형 동적해석이나 특별한 감쇠장치가 포함되어 감쇠를 강성과 질량의 선형조합으로 가정할 수 없을 경우에는 사용할 수 없습니다. Direct Integration : 직접적분법 동적평형방정식을 시간에 따라 점진적으로 적분하여 해를 구하는 방법입니다. 평형방정식의 형태 변화없이 시간단계마다 적분을 사용하여 해를 구하게 되고 사용방법에 따라 다양한 적분방법이 사용될 수도 있습니다. midas Gen에서는 수렴성이 좋은 Newmark 방법을 사용하여 직접적분법을 수행하고 있습니다.
강성이나 감쇠의 비선형성을 고려한 해석을 위해서는 대부분의 경우 직접적분법을 사용해야 합니다. 직접적분법의 경우는 모든 시간단계에 대하여 해석을 수행하기 때문에 시간단계의 수에 비례하여 해석시간이 소요됩니다. Static : 정적해석 Note
Transient : 시간이력해석을 수행할 하중을 재하시간동안 한번만 재하되는 하중으로 고려합니다. 일반적인 지진하중에 대해서 시간이력해석을 수행할 때 선택합니다. Periodic : 시간이력해석에 적용될 하중이 End Time과 동일한 주기를 가지고 반복 재하된다고 가정합니다. 기계진동 하중과 같이 일정한 주기를 가지며 반복해서 작용하는 하중에 대한 시간이력해석을 수행할 때 선택합니다.
시간이력해석에서 대변형에 의한 기하비선형효과를 고려하는 경우에 선택합니다. Analysis Type이 Nonlinear’이고, Analysis Method 가 ‘Direct Integration’ 또는 ‘Static’일 경우에만 사용할 수 있습니다.
해석하고자 하는 종료시간이나 해석횟수 Note
해석에 사용되는 시간간격으로 해석의 정확성에 상당한 영향을 미칠 수 있으며, 시간간격의 크기는 구조물의 고차모드의 주기나 하중의 주기와 밀접한 관계를 갖습니다. 일반적으로 고려하고자 하는 최고차모드 주기의 1/10정도의 시간간격이 타당합니다. 또한 해석시간 간격은 입력된 하중의 시간간격보다는 작아야 합니다.
구조물에 재하될 하중까지의 증분간격을 입력합니다. 예를들어, 증분스텝수가 100이고 재하될 하중이 100tonf이라면 비선형 정적해석시 하중은 1tonf씩 증가하며 각 Step에 대하여 해석을 수행합니다.
시간이력해석 결과를 출력하기 위한 시간간격을 입력합니다. 예를 들어, End Time이 1초, Time Increment가 0.01초라면 총 Step수는 100개 입니다. Step Number Increment for Output 에 2를 입력하셨다면 0.02, 0.04, 0.06...과 같이 두 스텝마다 한번씩 결과를 출력합니다. |
Order in Sequential Loading |
복수의 시간이력해석조건을 사용하여 연속적으로 재하되는 동적하중에 대한 해석을 수행함에 있어서 재하 순서와 관련한 데이터를 입력합니다.
현재 입력중인 시간이력해석조건에 선행하는 해석조건으로서 이미 입력된 시간이력해석조건을 선택합니다. 이때 선택 가능한 시간이력해석조건은 Analysis Type과 Analysis Method가 동일한 해석조건으로 제한됩니다. 선택된 선행 해석조건으로부터 변위, 속도, 가속도, 부재력, 힌지상태변수, 비선형연결요소 상태변수를 이어받아 초기조건으로 간주하고 해석을 수행합니다. 그러나 하중의 경우에는 Keep Final Step Loads Constantly를 체크한 경우에만 선행 해석조건의 최종상태에서의 하중이 현재의 해석조건에서 일정하게 지속된다고 가정합니다. Load Case : 선행하중조건을 선택합니다. 시간이력하중(TH) 뿐 아니라 정적하중(ST)과 시공단계하중(CS)도 고려할 수 있습니다. 자중과 같은 정적하중을 시간이력하중으로 치환하여 입력할 필요가 없으며 정적하중 케이스를 선택하여 자중을 고려할 수 있습니다. Initial Element Force (Table) : 선행하중조건에 의한 부재의 단면력을 고려합니다. Load Case를 선택하여 선행하중을 입력할 경우 동일한 구조계에서의 하중으로 제한되는 반면 Initial Element Force (Table)를 이용하면 지진시 해석과 같이 경계조건이 달라지는 구조물의 경우에 대해서 평형력의 형태로 선행하중을 입력할 수 있습니다. 또한 케이블 교량의 해체계산시 사용됩니다. Note 이 기능은 Initial Element Force 테이블에서 입력된 요소의 초기부재력을 선행하중 조건으로 고려한다. Equilibrium Member Force(Table) : 선행하중조건에 의한 부재의 단면력을 고려합니다. Load Case를 선택하여 선행하중을 입력할 경우 동일한 구조계에서의 하중으로 제한되는 반면 Equilibrium Element Nodal & Member Force를 이용하면 지진시 해석과 같이 경계조건이 달라지는 구조물의 경우에 대해서 평형력의 형태로 선행하중을 입력할 수 있습니다. 또한 케이블 교량의 해체계산시 사용됩니다. 또한, 선행하중조건에 의한 부재력이 탄성범위인 경우에만 적용되며, 탄성범위를 넘는 경우에는 부적절한 결과가 나올수 있습니다.
Initial Load(Global Control) : Global Control 에서 설정한 초기하중 적용
|
Damping |
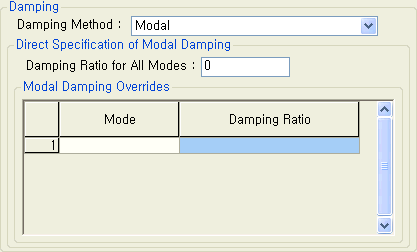
Direct Specification of Modal Damping : 모드별 감쇠비를 직접 정의합니다. Damping Ratio for All Modes : 사용자에 의하여 직접 입력된 모드별 감쇠비를 제외한 전체모드에 대하여 기본적으로 적용되는 감쇠비입니다. 아래 Modal Damping Overrides 입력란에서 지정한 특정모드의 감쇠비를 제외한 나머지 모드에 모두 적용됩니다. Modal Damping Overrides : 사용자가 직접 모드별 감쇠비를 별도로 입력하는데 사용합니다. Mode : 모드번호 Damping Ratio : 모드별 감쇠비
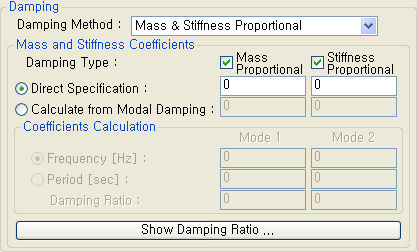
Damping Type : 감쇠행렬이 질량(Mass Proportional)에 비례하는 형태인지, 강성(Stiffness Proportional)에 비례하는 형태인지를 체크합니다. Direct Specification : Damping Type에서 체크한 항목에 대해 비례계수를 직접 입력합니다. Calculate from Modal Damping : Coefficients Calculation에서 사용자가 지정한 모드감쇠비로부터 비례계수를 계산하여 자동 입력합니다. Coefficients Calculation : Damping Type의 체크항목에 따라 질량 또는 강성 중 한개 또는 두개의 모드 감쇠비를 지정할 수 있습니다. Frequency[Hz] : 비례계수의 계산을 위해 감쇠비를 지정할 모드의 진동수를 입력합니다. Period [Sec] : 비례계수의 계산을 위해 감쇠비를 지정할 모드의 주기를 입력합니다. Damping Ratio : 입력된 Frequency 또는 Period에 해당되는 모드의 감쇠비를 입력합니다.
Note
|
Static Loading Control [Nonlinear Static 해석 선택시 활성화] |
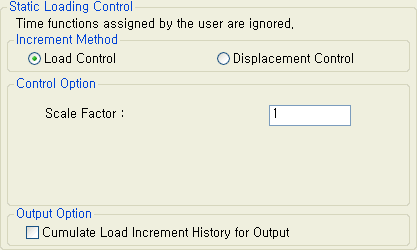
비선형 정적해석시 제어방법으로는 하중증분법(Load Control)과 변위증분법(Displacement Control)의 두 가지 가 있습니다. 전자는 하중을 단계별로 증가시키면서 최종하중에 도달할 때까지 해석을 수행하는 방법이며, 후자는 변위를 단계별로 증가시켜 목표변위에 도달함에 따라 해석이 종료되는 방법입니다. Note
Scale Factor : 비선형 정적해석에 사용되는 하중에 대한 증감계수 Cumulate Load Increment History for Output : 선행하중조건의 하중증분 결과를 누적하여 조합된 결과를 출력합니다.
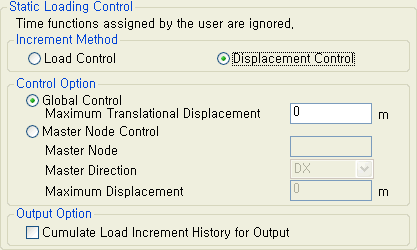
Global Control : 구조물에 발생하는 최대 변위가 사용자가 입력한 최대이동변위에 도달할 경우에 해석이 종료됩니다. Maximum Translational Displacement : 최대이동변위를 입력합니다. Master Node Control : 사용자가 선택한 주절의 변위가 입력된 최대변위에 도달할 경우에 해석이 종료됩니다. Master Node : 주절점의 절점번호를 입력합니다. Master Direction : 주절점의 최대변위를 제어할 방향을 선택합니다. Maximum Displacement : 주절점의 최대변위를 입력합니다. Cumulate Load Increment History for Output : 선행하중조건의 하중증분 결과를 누적하여 조합된 결과를 출력합니다. |
Time Integration Parameters |
Newmark Method : 직접적분법에서는 운동방정식의 수치적분을 위해 Newmark Method를 사용하고 있으며 이에 관련된 Gamma와 Beta의 두 개 파라미터를 입력합니다. 입력 방법은 다음 세 가지 옵션이 있으며 이 가운데 항상 안정적인 해석이 가능한 Constant Acceleration을 사용할 것을 권장합니다. Constant Acceleration : 구조물의 가속도가 각 Time Step의 시간 간격 동안에는 일정한 값으로 유지된다고 가정하며 이에 해당되는 Gamma(=1/2)와 Beta(=1/4)를 자동 입력해 줍니다. 이 가정에 의하면 직접적분에 의한 해석에 있어서 Time Increment의 값에 무관하게 해석결과의 발산을 막을 수 있습니다. Linear Acceleration : 구조물의 가속도가 각 Time Step의 시간 간격 동안에는 직선으로 변화한다고 가정하며 이에 해당되는 Gamma(=1/2)와 Beta(=1/6)를 자동 입력해 줍니다. 이 가정에 의하면 직접적분에 의한 해석에 있어서 Time Increment의 값이 구조물에 포함된 가장 짧은 주기의 0.551배 이상인 경우에 해석 결과가 발산할 수 있습니다. User Input : Gamma와 Beta의 값을 사용자가 직접 입력합니다. |
Nonlinear Analysis Control Parameters |
Analysis Type에서 Nonlinear를 선택한 경우에 비선형해석에 필요한 Parameter를 입력합니다.
Perform Iteration : Newton Raphson법을 이용하여, 수렴계산을 수행합니다. Iteration Controls : 비선형해석시 수렴해의 정확성 및 수렴성을 증진시키기 위한 방법을 설정합니다.
Iteration Parameters : 비선형동적해석시 수렴해의 정확성 및 수렴성을 증진시키기 위한 변수를 지정합니다. Permit Convergence Failure : 비선형 정적해석(Nonlinear-Static)을 수행할 경우 비활성됩니다. Minimum Substep Size : 각 해석시간단계(Time Step)를 세분한 하위 시간단계(Sub-step)의 최소값. Newton Raphson법을 이용한 수렴계산을 수행할 경우, 최대 반복 횟수만큼 반복계산을 수행하여도, Convergence Criteria에서 정의된 수렴 판정조건을 만족하지 못한 경우에는 자동으로 시간 간격을 세분하여, 정의된 수렴 판정조건이 만족할 때까지 계산을 수행합니다. Minimum Substep Size은 시간 간격을 세분할 때의 최소 간격을 의미합니다. Maximum Iteration : 각 하위시간단계별 최대 반복해석 횟수입니다. Analysis Method에서 Modal을 선택한 경우에는 E. L. Wilson이 개발한 Fast Nonlinear Analysis Algorithm에 의한 반복해석을 수행하며 Direct Integration을 선택한 경우에는 Newton Raphson 반복법을 수행합니다. 최대 반복 횟수는 10회 이하가 적절하며 지나치게 큰 값을 설정하면 해석시간이 길어지게 됩니다. Convergence Criteria
: 비선형 시간이력해석에서 적용되는 수렴판정기준을 지정합니다. Boundary Nonlinear Analysis : 경계비선형해석시 수렴해의 정확성 및 수렴성을 증진시키기 위한 수렴방법을 선택합니다. Runge Kutta Method : 요소 레벨에서 미분방정식을 풀때 증분시간을 자동으로 변환하여 해를 구하는 방법입니다. Fehlberg Method (Stepsize sub-division for Non-convergence Control) Cash-Karp
Method(Adaptive Stepsize Control)
Perform Iteration : Newton Raphson법을 이용하여 수렴계산을 수행합니다. Damping Matrix Update : 비선형 시간이력해석 중에서 직접적분법을 이용하는 경우에 강성변화에 따라서 요소의 감쇠행렬을 계속적으로 변화시키며 해석을 수행할지에 대한 여부를 선택합니다. Damping Matrix Update을 선택하지 않으면 탄성상태의 초기강성을 이용하여 요소의 감쇠 행렬을 산정하고 Damping Matrix Update을 선택하면 강성이 변화된 현재상태의 요소행렬을 이용하여 요소의 감쇠 행렬을 산정합니다. Damping Matrix Update는 Mass and Stiffness Proportional, Element Mass & Stiffness Proportional인 경우 지정가능합니다. Iteration Controls : 비선형해석시 수렴해의 정확성 및 수렴성을 증진시키기 위한 방법을 설정합니다.
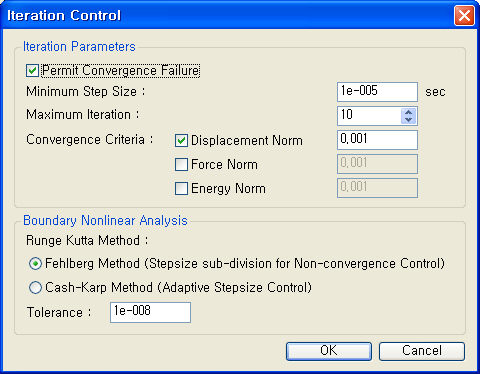
Iteration Parameters : 비선형동적해석시 수렴해의 정확성 및 수렴성을 증진시키기 위한 변수를 지정합니다. Permit Convergence Failure : Newton Raphson법을 이용한 수렴계산시, 최대 반복 횟수만큼 반복계산을 수행하여도, Convergence Criteria에서 정의된 수렴 판정조건을 만족하지 못한 경우, 메시지 출력후 종료됩니다. Permit Convergence Failure을 Check On하면, 수렴 판정조건을 만족하지 못한 경우도, 계속 계산을 수행할 수 있습니다. 동적 비선형 해석시 비선형 거동에 의해 강성변화가 매우 큰 경우 Permit Convergence Failure를 Check On한 상태로 얻어진 결과는 완전히 수렴되는 못한 상태의 결과일 수 있습니다. 이런 경우는 시간 간격을 좀더 작게 조정하여 계산을 수행하시기 바랍니다. Minimum Step Size : 각 해석시간단계(Time Step)를 세분한 하위 시간단계(Sub-step)의 최소값. Newton Raphson법을 이용한 수렴계산을 수행할 경우, 최대 반복 횟수만큼 반복계산을 수행하여도, Convergence Criteria에서 정의된 수렴 판정조건을 만족하지 못한 경우에는 자동으로 시간 간격을 세분하여, 정의된 수렴 판정조건이 만족할 때까지 계산을 수행합니다. Minimum Substep Size은 시간 간격을 세분할 때의 최소 간격을 의미합니다. Maximum Iteration : 각 하위시간단계별 최대 반복해석 횟수입니다. Analysis Method에서 Modal을 선택한 경우에는 E. L. Wilson이 개발한 Fast Nonlinear Analysis Algorithm에 의한 반복해석을 수행하며 Direct Integration을 선택한 경우에는 Newton Raphson 반복법을 수행합니다. 최대 반복 횟수는 10회 이하가 적절하며 지나치게 큰 값을 설정하면 해석시간이 길어지게 됩니다. Convergence Criteria
: 비선형 시간이력해석에서 적용되는 수렴판정기준을 지정합니다. Boundary Nonlinear Analysis : 경계비선형해석시 수렴해의 정확성 및 수렴성을 증진시키기 위한 수렴방법을 선택합니다. Runge Kutta Method : 요소 레벨에서 미분방정식을 풀때 증분시간을 자동으로 변환하여 해를 구하는 방법입니다. Fehlberg Method (Stepsize sub-division for Non-convergence Control) Cash-Karp
Method(Adaptive Stepsize Control)
Perform Iteration : Newton Raphson법을 이용하여, 수렴계산을 수행합니다. Iteration Controls : 비선형해석시 수렴해의 정확성 및 수렴성을 증진시키기 위한 방법을 설정합니다.
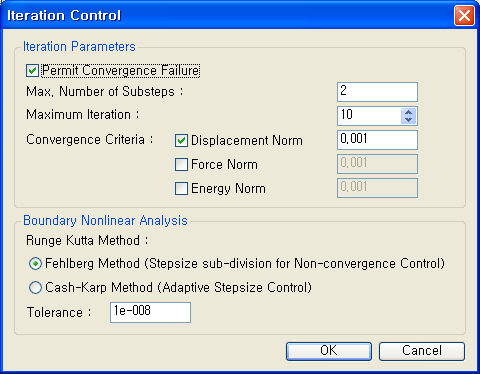
Iteration Parameters : 비선형 정적해석시 수렴해의 정확성 및 수렴성을 증진시키기 위한 변수를 지정합니다. Permit Convergence Failure : Newton Raphson법을 이용한 수렴계산시, 최대 반복 횟수만큼 반복계산을 수행하여도, Convergence Criteria에서 정의된 수렴 판정조건을 만족하지 못한 경우, 메시지 출력후 종료됩니다. Permit Convergence Failure을 Check On하면, 수렴 판정조건을 만족하지 못한 경우도, 계속 계산을 수행할 수 있습니다. 동적 비선형 해석시 비선형 거동에 의해 강성변화가 매우 큰 경우 Permit Convergence Failure를 Check On한 상태로 얻어진 결과는 완전히 수렴되는 못한 상태의 결과일 수 있습니다. 이런 경우는 시간 간격을 좀더 작게 조정하여 계산을 수행하시기 바랍니다. Max. Number of Substeps : Maximum Iteration : 각 하위시간단계별 최대 반복해석 횟수입니다. Analysis Method에서 Modal을 선택한 경우에는 E. L. Wilson이 개발한 Fast Nonlinear Analysis Algorithm에 의한 반복해석을 수행하며 Direct Integration을 선택한 경우에는 Newton Raphson 반복법을 수행합니다. 최대 반복 횟수는 10회 이하가 적절하며 지나치게 큰 값을 설정하면 해석시간이 길어지게 됩니다. Convergence Criteria
: 비선형 시간이력해석에서 적용되는 수렴판정기준을 지정합니다. Note Note |
: 입력된 비례계수로부터 특정 진동수 혹은 주기를 가진 모드의 감쇠비를 계산해서 보여주는 Damping
Ratio 대화상자가 활성화 됩니다. 질량 및 강성에 비례하는 감쇠를 사용하는 경우 최대 2개의
모드에 대해서만 감쇠비를 지정할 수 있으므로 다른 나머지 모드에 대해서는 어느정도의 감쇠비가 반영되는지를
간단히 계산해 볼 수 있는 기능입니다.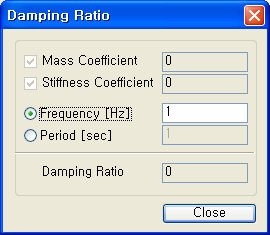
.bmp)
|
