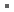 힌지
컴포턴트 (단일) 힌지
컴포턴트 (단일)
hysteresis
모델
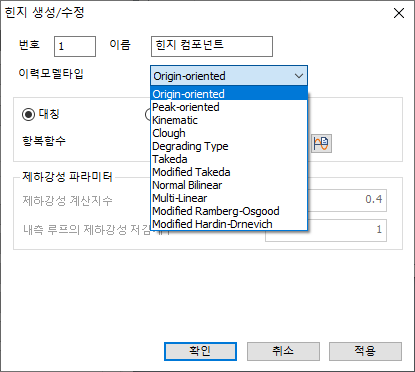
- Origin-oriented
: 초기 재하 시의 응답점은 골격 곡선 상에서 이동합니다. 제 1차
항복 이후에 제하되는 경우 원점을 지향하는 직선 상으로 이동합니다.
제하 과정에서 재재하 되는 경우는 제하 시와 같은 기울기의 직선 상으로
이동하고 골격 곡선과 만나면 골격 곡선 상에서 이동합니다.
-
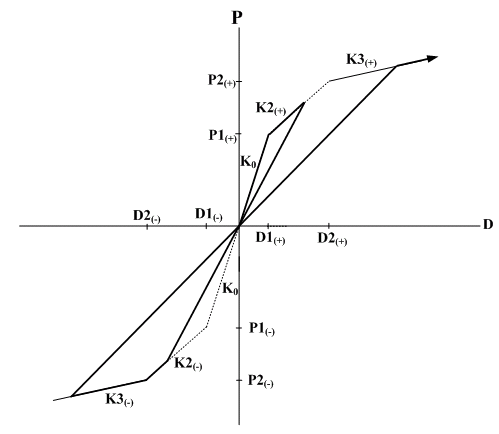
Peck-oriented : 초기
재하 시의 응답점은 골격 곡선 상에서 이동합니다. 제 1차 항복 이후에
제하되는 경우 반대측의 최대 변형점을 지향하는 직선 상으로 이동합니다.
만약 반대측이 1차 항복점을 지나지 않은 경우는 1차 항복점이 최대
변형점이 됩니다. 제하과정에서 재재하되는 경우는 제하시와 같은 기울기의
직선 상으로 이동하고 골격 곡선과 만나면 골격 곡선 상에서 이동합니다.
-
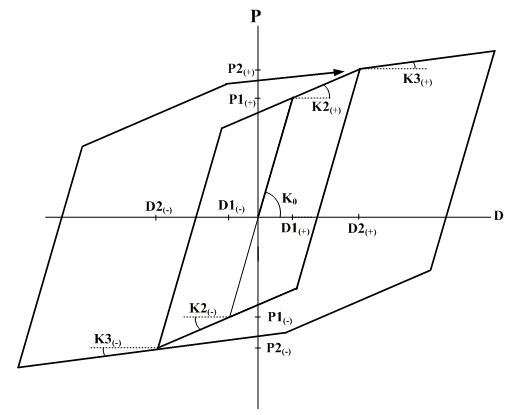
Kinematic
:
초기 재하 시의 응답점은 3선형 골격 곡선 상에서 이동합니다. 제하
강성은 탄성 강성과 동일합니다. 하중이 증가함에 따라 강도가 증가하는
경향을 보여줍니다. 이것은 금속 재료의 Bauschinger 효과를
모델링하는 데 사용됩니다. 따라서 콘크리트의 경우 에너지 손실이 과대평가될
수 있음을 주의해야 합니다. 모델의 특성 상 항복 후 강도 감소율은
양 (+) 및 음 (-) 대칭만 허용됩니다.
-
Clough : 초기
재하 시의 응답점은 골격 곡선 상에서 이동하며 항복 후에는 변형의 진전에
의해 재하 강성이 점진적으로 감소하는 형태입니다. 콘크리트는 건조 수축
등에 의해 균열이 발생하기 쉬우므로 균열 전의 상태는 무시하고 전체
단면에 균열이 발생한 것으로 간주하여 인장 철근의 휨항복에 의한 강성
변화만을 고려하도록 고안된 모델입니다.
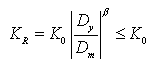
여기서,
KR
: 제하 시 강성
Ko
: 탄성 강성
Dy
: 제하가 시작되는 구역의 항복 변위
Dm
: 제하가 시작되는 구역의 최대 변위
(항복이
발생하지 않은 영역에서 항복 변위로 대체)
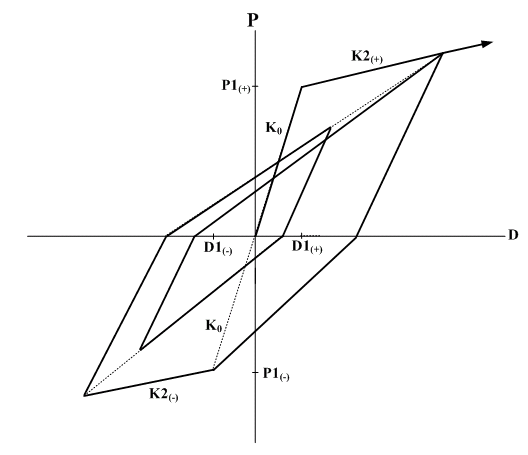
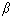 : 제하 강성을 결정하기 위한 상수 : 제하 강성을 결정하기 위한 상수
제하
과정에서 하중의 부호가 바뀌면 진행 방향 영역에서 최대 변위점을 향하여
응답점이 이동합니다. 이 영역에서 항복이 발생하지 않으면 응답점은 골격
곡선의 항복점을 향해 이동합니다. 로딩 부호를 변경하지 않고 언로딩이
로딩이 되면 언로딩 경로를 따라 응답점이 이동합니다. 하중이 계속 증가하면
다시 골격 곡선에 하중이 계속됩니다.
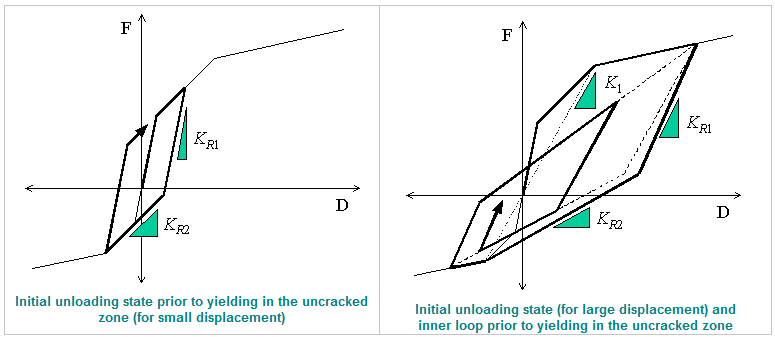
- Degrading
:
초기 하중에서의 응답점은 삼선형 골격 곡선을 따라 이동합니다. 제하
시 하중-변위 좌표는 중간에 한번 제하 강성의 변화로 인해 반대측에서
최대 변형점에 도달하는 경로로 이동한다. 반대쪽에서 항복이 발생하지
않은 경우 첫 번째 항복점을 최대 변형점으로 가정합니다.
-
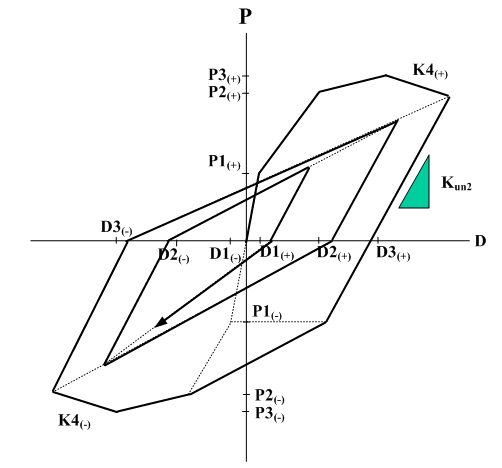
Takeda
:
초기 하중에서의 응답점은 사선형 골격 곡선을 따라 이동합니다. 현재
변위 또는 변형 D가 D3를 초과하지 않으면 hysteresis 규칙은
원래 Taketa hysteresis와 동일합니다. 현재 변위 또는
변형 D가 D3을 초과하면 응답점이 기울기 K4를 따라 이동합니다.
제하의 경우 응답점은 Original Taketa hysteresis
와 동일한 규칙으로 이동합니다. Takeda 사선형 hysteresis
모델은 집합형과 분산형의 스프링형의 보요소와 일반 링크에 적용할 수
있습니다.
-
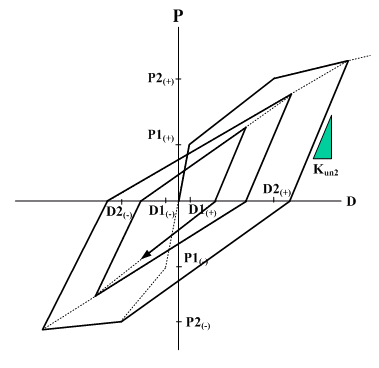
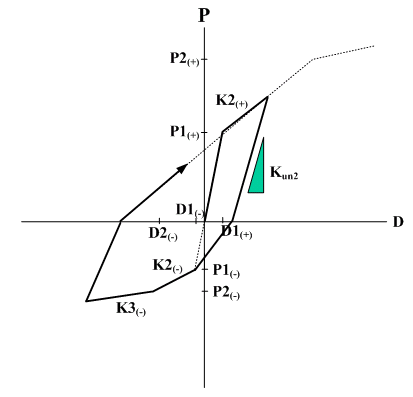
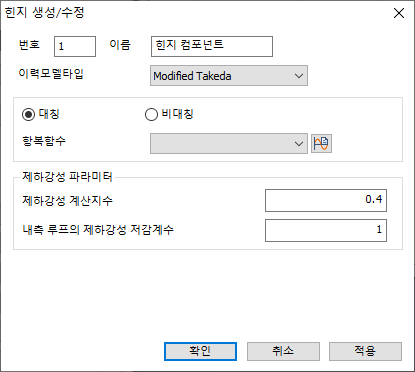
Modified Takeda : 초기
하중에서의 응답점은 삼선형 골격 곡선을 따라 이동합니다. 현재 변위
또는 변형 D가 처음으로 D2를 초과하거나 지금까지의 최대 변형점을
초과하면 응답점이 삼선형 골격 곡선을 따라 이동합니다. 이 직선에서
반대방향으로 제하가 일어나면 복원력이 0이 되는 지점까지 기울기 Kun2를
따라 점들이 이동한다. 복원력이 0점을 넘어서면 점들은 위의 최대 변형점으로
이동한다. 반대편. 복원력이 0인 점에서 최대 변형점을 향하는 직선에서
제하가 발생하는 경우에도 점들은 복원력이 0이 될 때까지 기울기 Kun2를
따라 이동한다. 복원력이 0인 지점을 지나면 반대측의 최대 변형 지점을
향해 지점이 이동합니다. Modified Takeda 형 hysteresis
모델은 Lumped Type과 Distributed Type의 Spring
Type의 Beam 요소와 General Link에 적용할 수 있습니다.
- Normal
Bilinear :
초기 재하 시의 응답점은 2선형 뼈대 곡선 (Skeleton Curve)
상에서 이동합니다. 제하 (unloading) 강성은 탄성 강성과 동일합니다.
Normal Bilinear 형 hysteresis
모델은 집중형과 분산형의 스프링 형태의 보 요소와 일반적인 링크에 적용할
수 있습니다.
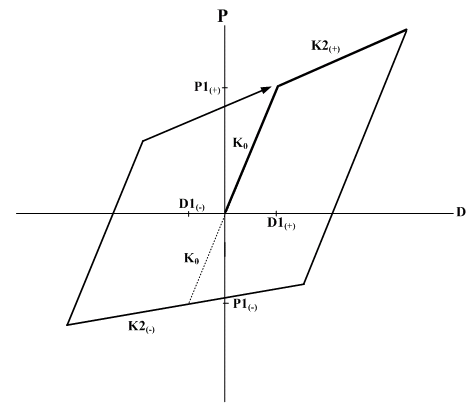
-
Modified Ramberg-Osgood :

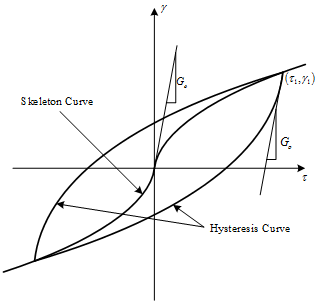
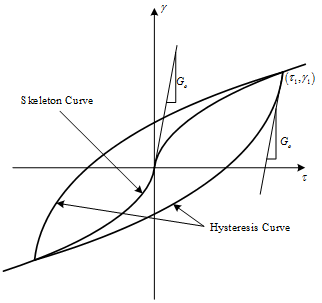
-
Modified Hardin-Drnevich :

Symmetric
/ Asymmetric
: 골격선의 형태를 선택합니다.
Yield
Function
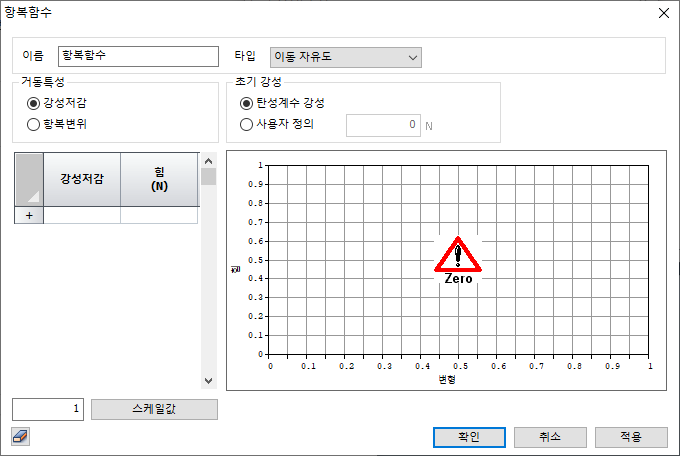
- 감성 저감율
: Input Type 에서 Strength - Stiffness Reduction
Ratio 를 선택한 경우 경사진 골격 곡선의 강성 저감율을 입력합니다.
- 항복 변위 : 입력 유형으로
강도 - 항복 변위를 선택한 경우 경사 골격 곡선의 항복 변위를 입력합니다.
- Force (항복 강도)
: 항복 강도를 지정합니다. 재료 및 단면 속성을 기반으로 사용자 정의됩니다.
사용자는 장력 (t) 또는 압축 (c)에 관계없이 양수 (+) 값을
지정합니다. 프로그램은 내부적으로 압축을 음수 (-)로 처리합니다.
제하
강성 파라미터
제하 강성 계산의 성분:
골격 곡선의 hysteresis 모델 중 Clough 및 Takeda
유형 모델에서 사용되는 외부 루프의 제하 강성을 결정하는 데 사용되는
옵션입니다. 이는 항복 후 변형이 진행됨에 따라 발생하는 강성 감소
효과를 반영하기 위해 사용됩니다. 제하 강성은 제하가 시작되는 구역과
여기에 입력된 지수의 항복 변위와 최대 변위만큼 감소된 탄성 강성에
의해 결정됩니다.
내부 루프 제하 강성
감소 계수: 내부 루프의 제하 강성을 결정하는 데 사용됩니다.
제하 과정에서 부하 부호가 변한 후 재부하동안 Skeleton Curve
상의 목표점에 도달하기 전에 제하가 발생하면 내부 루프가 형성된다.
내부 루프의 제하 강성은 외부 루프의 제하 강성에 내부 루프의 제하
강성에 대한 감소율을 곱하여 계산됩니다.
 힌지
컴포턴트 (다중) 힌지
컴포턴트 (다중)
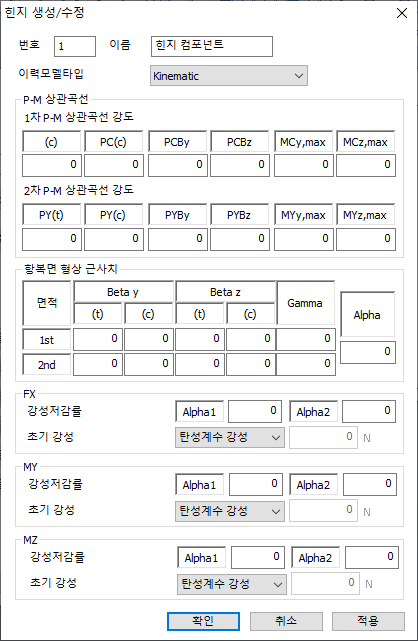
- P-M
상관 곡선 : 3차원 항복면을 계산하는 데 필요한 P-M 상호 작용
곡선 데이터를 입력합니다. 모든 강도 값은 양수 기호로 입력해야 합니다.
P-M 곡선을 그리는 기호 규칙은 압축에 대해 양수이고 장력에 대해
음수입니다.
1차
P-M 상관 곡선 강도
PC
(t) : 순수 인장력에 대한 1차 항복 강도
PC
(c) : 순수 압축력에 대한 1차 항복 강도
PCBy
: 단면의 y축-휨에 대한 1차 항복 상관 곡선에서 균형 파괴
발생 시의 축력
PCBz
: 단면의 z축-휨에 대한 1차 항복 상관 곡선에서 균형 파괴
발생 시의 축력
MCy,
max: 단면의 y축-휨에 대한 1차 항복 상관 곡선에서 최대
휨 항복 강도
MCz,
max:
단면의 z축-휨에 대한 1차 항복 상관 곡선에서 최대 휨 항복 강도
2차
P-M 상관 곡선 강도
PY
(t) : 순수 인장력에 대한 2차 항복 강도
PY
(c) : 순수 압축력에 대한 2차 항복 강도
PYBy
: 단면의 y축-휨에 대한 2차 항복 상관 곡선에서 균형 파괴
발생 시의 축력
PYBz
: 단면의 z축-휨에 대한 2차 항복 상관 곡선에서 균형 파괴
발생 시의 축력
MYy,
max : 단면의 y축-휨에 대한 2차 항복 상관 곡선에서 최대
휨 항복 강도
MYz,
max : 단면의 z축-휨에 대한 2차 항복 상관 곡선에서 최대
휨 항복 강도
- 항복면
형상 근사치 : P-M 상호 작용 곡선을 기반으로 3차원 항복면에 대한
매개변수는 사용자가 정의하거나 자동으로 계산됩니다. 일부 항복은 자동
계산 되고 나머지는 사용자 정의일 경우 자동 계산을 먼저 수행한 후
사용자 입력으로 변환하여 필요한 항복을 수정할 수 있습니다. 알파의
경우 사용자 정의 입력만 가능합니다. 각 매개변수의 값은 대화상자에
표시되는 항복면 방정식에 사용됩니다.
Beta
y, Beta z, Gamma : P-My 또는 P-Mz 상관
관계의 차수로 1차 및 2차 항복에 대해 다른 값을 입력 가능합니다.
또한 Beta y, Beta z는 균형 파괴 발생 시 축력을 기준으로
그보다 큰 축력과 작은 축력의 영역에 대해 서로 다른 2개 값을 입력할
수 있습니다.
Alpha
: 1차 및 2차 항복에 대한 My-Mz 상관 관계의 차수입니다.
-
강성
저감률:
Input Type 에서 강성 저감률을 선택한 경우 경사 뼈대 곡선의
강성 감소 비율을 입력합니다.
α1
: 최초 항복 직후의 강성을 초기 강성으로 나눈 비율
α2
: 2차 항복 직후의 강성을 초기 강성으로 나눈 비율
- 초기 강성
: 비탄성 해석에 사용되는 초기 강성을 선택하거나 사용자가 직접 입력합니다.
탄성
계수 강성 : 요소에 정의된 탄성 계수를 초기 강성으로 사용합니다.
사용자
정의 :
Stiffness Reduction 타입일 때에만 사용 가능하며, 사용자가
초기 강성을 직접 입력합니다.
|


![]()