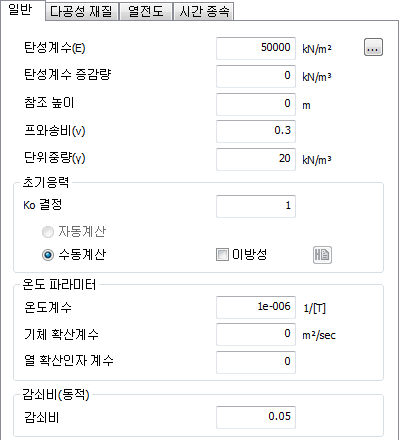
기본 파라미터 (일반)
재료
모델별 기본 강성 및 초기조건을 정의하는 입력 파라미터와 단위는 아래 테이블과 같습니다.
입력파라미터 |
설명 |
단위 |
탄성계수(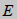 ) ) |
탄성계수 |
kN/m2 |
탄성계수
증감량 |
높이에
따른 탄성계수의 증감량 (기울기) |
kN/m3 |
참조높이 |
탄성계수
증감 기준 높이 |
m |
프와송비(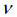 ) ) |
프와송
비 |
- |
단위중량
(γ) |
불포화
상태의 전체단위중량 (γt) |
kN/m3 |
초기응력
(Ko) |
정지토압계수(초기응력계산 파라미터) |
- |
온도계수 |
온도하중
계산을 위한 계수 |
1/[T] |
기체 확산계수 |
다공성 매질의 기체확산계수 |
m2/sec |
열
확산인자 계수 |
온도구배에
따른 기체의 흐름제어 계수 |
- |
감쇠비 |
재료
감쇠비(동해석에만
적용) |
- |
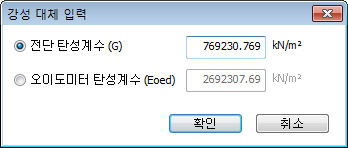
[탄성계수(E)]
재료의
기본 초기강성을 정의하기 위한 파라미터 입니다. 탄성계수를 정의하거나, Oedometer Test를
통해 구한 전단강성계수(G) 와 오이도미터 탄성계수(Eoed)로 대체할 수 있습니다. 지반재료는
대부분 하중재하 초기단계부터 비선형 거동을 보이기 때문에 초기 강성 입력이 매우 중요합니다. 아래
그림과 같이 삼축압축 시험결과 응력-변형률 곡선으로부터 초기 강성을 정의할 수 있는데, 큰 변형이
발생할때까지 선형(탄성)거동을 보이는 재료의 경우 E0를 쓰는 것이 현실적 이지만, 일반적인 지반재료에서는
E50, 즉 50% 응력 수준에서의 접선의 기울기를 초기 강성으로 사용하는 것이 적절합니다. 또한
일반적인 시공단계 해석에서 굴착에 의한 unloading과 reloading을 모사할 경우E50대신
Eur을 사용하는 것이 보다 현실적인 지반거동을 모사하는데 도움이 됩니다.
따라서,
일정한 초기강성을 이용하여 지반거동을 모사할 경우에는 지반이 받는 응력의 범위(크기)와 응력이동
경로에 따라 결정하는 것이 중요하며, 이와 같은 상세거동을 모사하기 위해 다양한 비선형 재료모델을
사용할 수 있습니다.
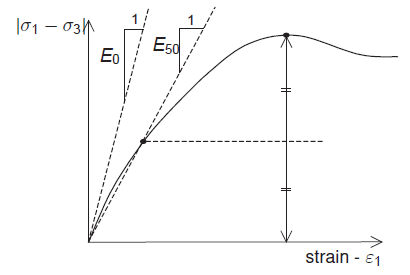
<삼축 압축시험 결과 그래프>
지반이
갖는 연속체의 특성상 체적탄성계수 K(bulk modulus)와 전단탄성계수 G(shear modulus)는
다소 논란의 여지는 있을 수 있지만, E와 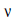 보다 간결하고 명확하게
표현될 수 있기 때문에 보다 편리하게 이용될 수 있습니다. 아래 그림은 K와 G가 가지는 역학적
의미를 간결하게 설명한 것입니다. 보다 간결하고 명확하게
표현될 수 있기 때문에 보다 편리하게 이용될 수 있습니다. 아래 그림은 K와 G가 가지는 역학적
의미를 간결하게 설명한 것입니다.
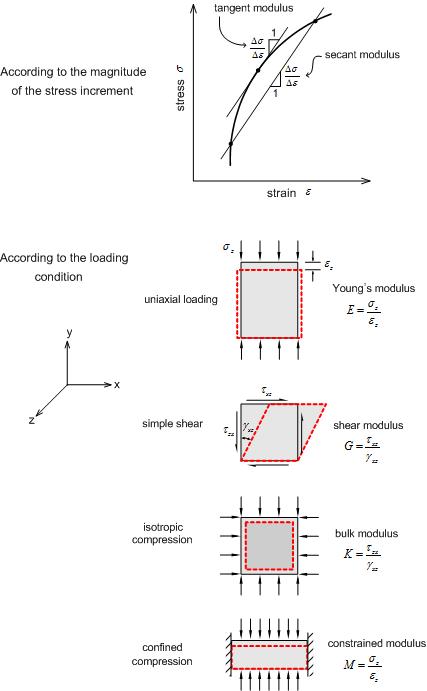
<다양한 종류의 탄성계수>
현장시험에
따라 얻는 탄성계수는 앞서 언급한 여러 가지 탄성계수 중 하나가 될 수 있으며, 적절하게 변환함으로써
실무에 적용할 수 있습니다.
지반재료 |
탄성계수
(tonf/m2) |
프이송
비 |
amphibolite |
9.4~12.1
´106 |
0.28~0.30 |
anhydrite |
6.8
´106 |
0.30 |
siabase |
8.7~11.7
´106 |
0.27~0.30 |
siorite |
7.5~10.8
´106 |
0.26~0.29 |
solomite |
11.0~12.1
´106 |
0.30 |
sunite |
14.9~18.3
´106 |
0.26~0.28 |
deldspathic
gneiss |
8.3~11.9
´106 |
0.15~0.20 |
gabbro |
8.9~11.7
´106 |
0.27~0.31 |
granite |
7.3~8.6
´106 |
0.23~0.27 |
ice |
7.1
´106 |
0.36 |
limestone |
8.7~10.8
´106 |
0.27~0.30 |
marble |
8.7~10.8
´106 |
0.27~0.30 |
mica
Schist |
7.9~10.1
´106 |
0.15~0.20 |
obsidian |
6.5~8.0
´106 |
0.12~0.18 |
oligoclasite |
8.0~8.5
´106 |
0.29 |
quartzite |
8.2~9.7
´106 |
0.12~0.15 |
rock
salt |
3.5
´106 |
0.25 |
slate |
7.9~11.2
´106 |
0.15~0.20 |
aluminum |
5.5~7.6
´106 |
0.34~0.36 |
steel |
20.0
´106 |
0.28~0.29 |
<암석 및 기타재료의 탄성계수와 포아송 비>
위
표에 나와있는 탄성계수는 균열이 없는 작은 시험체에 대한 실험실 값으로 무결암(intact rock)의
탄성계수에 해당합니다. 따라서, 현장을 고려하여 탄성계수를 적용할 때에는 대형 스케일의 암반 내
불연속면을 고려하여 감소된 탄성계수 값을 적용해야 합니다. 아래그림은 RQD(Rock Quality
Designation)에 따른 탄성계수 감소비를 나타낸 실측 데이터를 그래프로 표현한 것입니다.
RQD란 균열이 포함된 시추코아 100cm 길이에서 10cm 길이를 초과하는 코어 조각 길이의 합을
전체길이에 대한 백분율로 표현한 값입니다. RQD가 100%라고 해서 무결암이라고 볼 수는 없습니다.
그러나, RQD가 높을수록 암질은 우수하다고 볼 수 있으며, 풍화가 많이 진행된 암반일수록 RQD의
수치가 작아집니다.
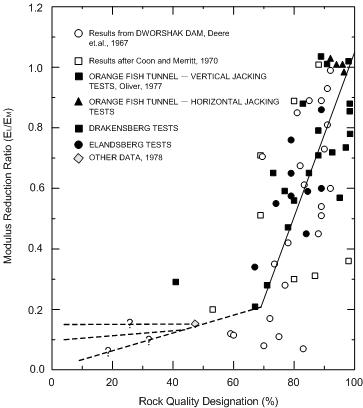
<RQD와 탄성계수 감수비융(EL/EM)과의 관계>
위
그림에서처럼 RQD가 70%만 되어도 실험실 탄성계수를 20%로 감소해야 함을 알 수 있습니다.

[탄성계수
증감량]
일반적으로
지반은 같은 재질의 층이라해도 깊이에 따라 구속압이 커지는 만큼 강도특성또한 변하는 특성이 있습니다.
이와 같은 특징을 해석에 반영하기 위해 참조높이(기준높이)를 기준으로 깊이에 따라 일정한 탄성계수
증감을 모사할 수 있습니다. 높이에 대한 탄성 증가량이 ‘0(zero)’이면 탄성계수는 일정한 값으로
사용되고 ‘0(zero)’이 아니면 기준 높이에 대해 탄성계수는 아래식과 같이 계산됩니다.
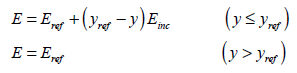
여기서,
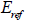 : 입력된 탄성계수 값 : 입력된 탄성계수 값
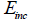 : 탄성계수의 증분 기울기 : 탄성계수의 증분 기울기
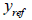 : : 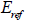 값을
측정한 깊이 값을
측정한 깊이
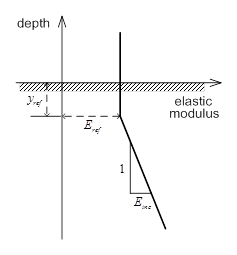
<탄성계수 즌분에 대한 개념도>
위의
식에서 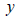 는 현재 유한요소법에서 계산이 진행되는 요소의 적분점
위치를 나타냅니다. 만약 적분점 위치가 는 현재 유한요소법에서 계산이 진행되는 요소의 적분점
위치를 나타냅니다. 만약 적분점 위치가 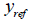 보다 높은 곳에 위치하는
경우는 위치에 따라 탄성계수값이 0보다 작아지는 경우가 발생하므로 이를 방지하기 위해 탄성계수 보다 높은 곳에 위치하는
경우는 위치에 따라 탄성계수값이 0보다 작아지는 경우가 발생하므로 이를 방지하기 위해 탄성계수 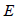 값을 더 이상 줄이지 않고 값을 더 이상 줄이지 않고 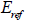 값을 사용합니다. 값을 사용합니다.
[프와송비(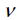 )] )]
탄성계수와
함께 응력과 변형률 관계에서 비례상수에 해당하는 계수로, 하중에 의한 재료의 체적변화율로 볼 수
있습니다. 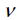 가 0.5에 근접할 수 록 비압축성(Incompressible)
고체를 의미하며, 0에 가까울수록 작은 하중에도 체적변화가 크게 나타나는 압축성 재료를 의미합니다.
자중에 의한 초기응력비인 K0 = σh/ σv 와도 일축압축 상태에서는 K0 = 가 0.5에 근접할 수 록 비압축성(Incompressible)
고체를 의미하며, 0에 가까울수록 작은 하중에도 체적변화가 크게 나타나는 압축성 재료를 의미합니다.
자중에 의한 초기응력비인 K0 = σh/ σv 와도 일축압축 상태에서는 K0 = 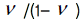 의 관계로 결정할 수
있습니다. 원지반 초기응력 계산시 K0 를 사용하지 않을경우 입력된 의 관계로 결정할 수
있습니다. 원지반 초기응력 계산시 K0 를 사용하지 않을경우 입력된 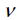 로
부터 수직응력에 대한 수평응력을 계산하게 됩니다. 지반재료의 일반적인 프와송비 범위는 0.3~0.4이내이며,
0.49보다 큰 수치를 입력할 경우에는 수치적인 오류를 발생시킬 수 있습니다. 따라서, 과압밀 상태의
지반처럼 K0 가 1이상인 경우에는 프와송비를 통해 계산될 수 없기 때문에 직접 수치를 입력해야
합니다. 로
부터 수직응력에 대한 수평응력을 계산하게 됩니다. 지반재료의 일반적인 프와송비 범위는 0.3~0.4이내이며,
0.49보다 큰 수치를 입력할 경우에는 수치적인 오류를 발생시킬 수 있습니다. 따라서, 과압밀 상태의
지반처럼 K0 가 1이상인 경우에는 프와송비를 통해 계산될 수 없기 때문에 직접 수치를 입력해야
합니다.
[전단탄성계수(G)]
탄성계수와
프와송비를 이용하여 Hooke's law에 따라 다음관계식으로 자동계산 되며, 탄성계수를 대체하는
용도로 직접 입력할 경우, 탄성계수가 바뀌게 됩니다.
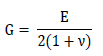

[오이도미터
탄성계수(Eoed)]
탄성계수와
프와송비로부터 Hooke's law에 따라 다음 관계식으로 계산될 수 있습니다.
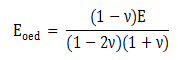
[초기응력(K0)]
정지토압계수로
초기원지반의 수직/수평응력 비를 의미하며 (K0
= σh/ σv), 전체좌표계 기준으로 이방성
특성을 설정할 수 있습니다.
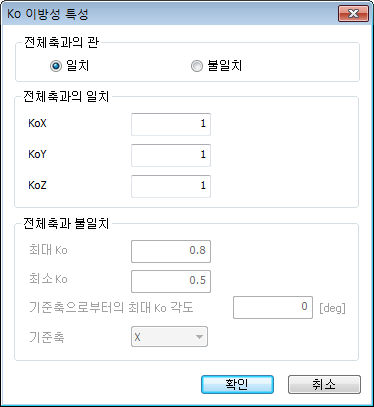
먼저,
전체좌표계 방향과 이방성 특성의 일치여부(일치/불일치)를 선택하고 선택한 옵션에 따라 각 축방향
또는 임의방향의 측압계수를 설정합니다.
전체축과 일치하는 경우 각 축방향 측압계수를
설정하되, 작업환경(2D/3D)에 따라 중력방향에 대해서는 '1' 이외의 값은 정의할 수 없습니다.
전체축과 불일치는 기준축을 중심으로
각도를 입력하여 최대 측압계수의 방향을 임의로 설정합니다. 기준축은 최대 측압계수의 방향을 설정하기
위한 중심축으로 작업환경이 2D일 경우 'X-Y' 평면으로 고정되어 있으므로 'X'축만 선택할 수
있으며, 초기 지반의 전단응력은 모두 '0(zero)'가 되고 3D 일 경우 중력방향 이외의 축을
각각 선택할 수 있습니다. 예를들어, 중력방향이 'Z'축 이고 기준축을 'X'축으로 설정할 경우
각도는 'X-Z'평면상의 최대 측압계수 작용 각도를 입력하며, XY, YZ 방향의 초기 지반 전단응력은
모두 '0(zero)'가 됩니다.
원지반
상태, 즉 지반이 굴착이나 성토 등에 의해서 흙이 교란되지 않은 상태에 지반의 응력상태는 정지토압계수와
자중을 이용하여 나타낼 수 있습니다. 즉 대부분의 해석과정에서는 시공 1단계에서 원지반 형태를 모델링
한 후에 K0를
적용하는 것이 실제와 근접한 응력상태를 얻을 수 있습니다. 하지만, 일반적으로 평평한 지반에서는
K0를 이용하여
응력을 구하는 것이 맞지만, 경사진 지반에서는 K0를
이용하여, 응력을 산정한 후 추가의 시공단계를 설정하여, 평형에 맞게 수렴시키는 작업을 하는 것을
추천합니다. 보다 자세한 사항은 해석>해석제어(옵션)을 참고해 주시기 바랍니다.
[온도파라미터]
온도계수 : 열응력해석을
수행할 때 필수로 입력해야 할 파라미터로 열팽창에 의한 물체의 팽창 비율이며 보통 일정한 압력하에서
온도가 1°C 올라갈 때마다의 부피 증가율로 표시됩니다.
기체 확산계수 : 다공질
매질의 기체 확산계수이며, 시간에 따른 기체 밀도의 변화를 나타냅니다. “응력침투열완전연계”에서만
사용되는 파라미터입니다.
열 확산인자 계수 : 무차원으로
온도 구배에 따른 기체의 흐름정도를 제어하기 위한 계수입니다. “응력침투열완전연계”에서만 사용되는
파라미터입니다.
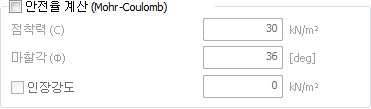
안전율
계산(Mohr Coulomb)
Mohr-Coulomb
파괴기준에 근거하여 재료의 응력상태가 얼마나 항복되어 있는지를 현재의 응력 상태와 파괴시의 응력상태에
대한 비율(안전율)로 출력해 주는 기능입니다. Mohr-Coulomb 파괴기준은 지반과 같은 취성재료에
가장 많이 적용되며, 별도의 계산식을 갖고 있는 D-min 재료모델과 von Mises, Tresca
에서는 사용할 수 없습니다.
- 점착력, 마찰각, 인장강도를
파괴기준으로 정의.
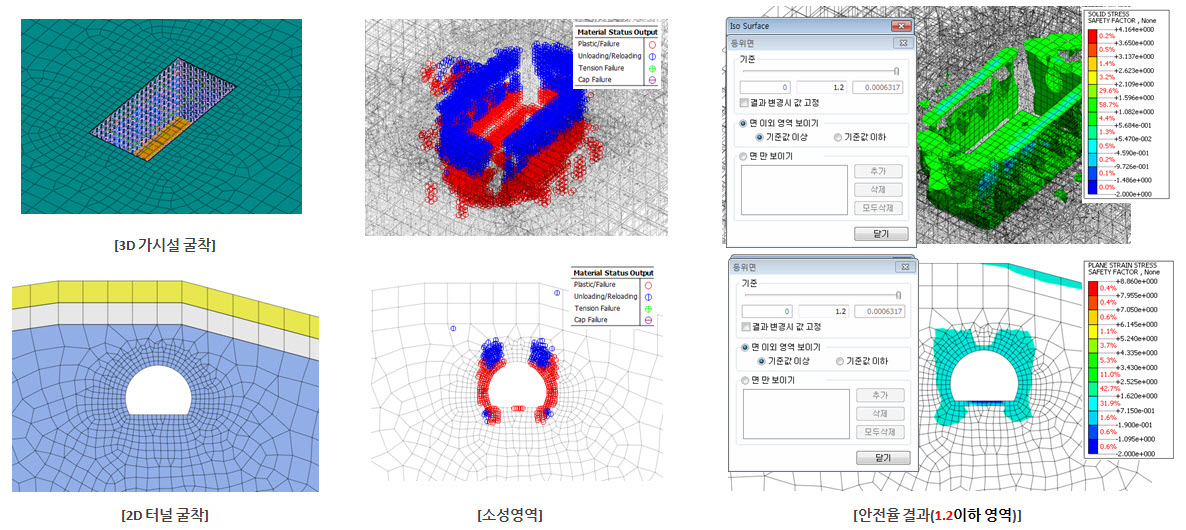
- 출력된 안전율로부터 안정한
영역과 소성파괴 영역을 직관적으로 확인할 수 있습니다.
- 안전율 결과는 결과트리에서
확인 가능.- (2D : Plain Strain Stresses > SAFETY
FACTOR , 3D : Solid Stresses > SAFETY FACTOR)
- 안전율이 1(혹은 1.2)
이하인 경우에는 소성파괴영역과 동일한 결과가 출력될 수 있음.
침투, 배수/비배수 파라미터
지반의
투수특성 및 배수/비배수 조건을 정의하는 입력 파라미터와 단위는 아래 테이블과 같습니다.
입력파라미터 |
설명 |
단위 |
단위중량(포화) |
포화상태
단위중량 |
kN/m3 |
초기공극비(eo) |
초기
간극비 |
- |
불포화특성 |
불포화특성
함수설정(음의간극수압-함수비-투수계수비) |
- |
배수
파라미터 |
배수/비배수 조건 |
- |
투수계수 |
전체좌표계
방향 -
포화상태 투수계수 |
m/sec |
공극비
의존 투수계수비(ck) |
공극비
변화에 따른 투수계수비 |
- |
비저류계수(Ss) |
유입/유출되는 물의
체적비 |
1/m |
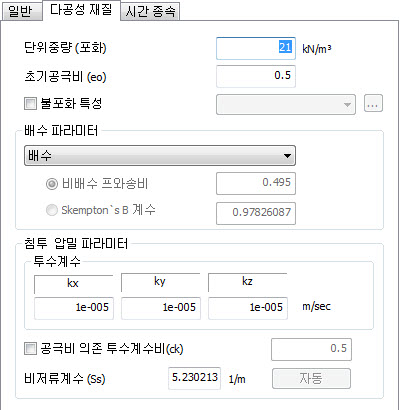
<투수파라미터>
[초기공극비(e0)]
압밀해석
및 응력-침투 완전연계 해석에 고려되는 지반의 초기 공극비 입니다. 흙속의 흙 입자 부분의 용적에
대한 공극의 용적비를 의미하며, 대개 지반에서 공극비는 1 이하입니다. 점토 혹은 유지질토가 되면
1보다 높을 수 있지만, 시료의 채취방법이나 진동/다짐 유무에 따라 변화하게 됩니다. 일반적으로
조립의 모래는 0.6~0.8정도이지만, 밀도가 높은, 입자분포가 좋은 모래는 0.3정도를 나타냅니다.
세립토의 경우 2~3까지 나타나는 경우도 있습니다.
[불포화
특성]
지반의
불포화특성을 고려하기 위해 설정합니다. 대표적으로 비정상류 침투해석에서 반드시 고려되어야 하는 특성이며,
이외 지반의 부분포화도를 고려한 비선형(시공단계)/압밀해석등을 수행할 때 설정합니다. 실제 지반은
포화상태보다는 대부분 일정비율의 공기를 함유하고 있는 불포화 상태이기 때문에, 보다 현실적인 해석결과
검토를 위해서는 불포화 특성이 고려된 비정상류 해석을 수행해야 합니다. 불포화 특성을 고려하지 않을경우
지반을 포화상태로 가정하고 해석을 수행하기 때문에 시간에 따른 침투해석 결과 변화를 검토할 수 없습니다.
불포화
특성은 지반의 불포화영역에서 음의간극수압 크기에 따른 투수계수 및 함수비(포화도) 변화를 정의하는
것으로 압력수두(음의간극수압)에 따른 투수함수 와 함수비 함수를 직접 정의(개별정의)하는 방법과,
압력수두-체적함수비(포화도)-투수계수비의 관계를 정의(관계정의)하는 방법이 있습니다.
보다
자세한 설명은 "함수>불포화특성
함수"를 참고해 주시기 바랍니다.

[배수
파라미터]
응력해석에서
간극수압은 정상상태 간극수압과 비정상상태, 즉 비배수 조건에 의해 외부작용하중을 흙 입자 사이의
물이 받게되는 과잉간극수압으로 나눌 수 있습니다. 과잉간극수압이 0에 가까운 상태를 배수조건이라
하며 일반적으로 모래와 같은 투수특성이 큰 지반재료에 대해서는 배수해석을 수행합니다. 하지만 점토와
같이 투수특성이 매우 작아 순간적으로 재하되는 하중에 의해 물이 미쳐 빠져나가지 못하는 비배수 거동을
모사할 경우 비배수 해석을 수행해야 하며, 과잉간극수압이 소산되기 전 초기 상태가 가장 불안정성한
상태라고 볼 수 있습니다. 이 때 간극수압은, 압축성에 따른 지반의 체적변화와 투수계수에 의해 결정됩니다.
비배수 프아송비와 Skempton(B) 계수는
물의 체적탄성계수를 계산하기 위한 파라미터로, 비배수 프와송비는 압축성이 '0(zero)'에 가까운
0.495를 기본값으로 사용하고, Skempton 인자는 포화된 정도를 나타내는 것으로 1에 가까울
수록 완전 포화상태를 의미합니다.
비배수
해석 수행시 재료의 종류는 아래와 같으며, 보다 자세한 구성방정식에 대한 설명은 해석메뉴얼Ch.4의
배수/비배수 재료를 반드시 참고해 주시기 바랍니다.
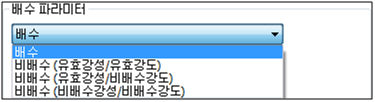
배수/비배수 재료 |
사용가능한
재료모델 |
배수 |
모든
지반재료 |
비배수(유효강성/유효강도) |
Elastic,
Mohr-Coulomb, Drucker-Prager, Duncan-Chang,
Hoek-Brown,
Strain Softening, Modified Cam-clay, Jardine,
D-min, Modified Mohr-Coulomb, User-supplied, Transversely
Isotropic |
비배수(유효강성/비배수강도) |
Mohr-Coulomb,
Drucker-Prager, Modified Mohr-Coulomb |
비배수(비배수강성/비배수강도) |
Elastic,
Mohr-Coulomb, Drucker-Prager, Modified Mohr-Coulomb |
[투수계수
(kx,ky,kz)]
침투해석과
압밀해석 수행시 사용되며, 지반의 투수특성(속도)을 나타내는 지표입니다. 전체좌표계의 각 방향별
투수계수를 정의할 수 있습니다. 입력된 수치는 포화상태일때의 투수계수로 불포화 특성함수 정의시 음의
간극수압에 따른 투수계수비(Kunsat / Ksat)를 산정하는 기준이 됩니다.
[공극비
의존 투수계수비 (ck)]
투수계수(permeability
coefficient)란 지반 내 지하수가 단위 시간에 대하여 얼마나 이동하는가에 대한 척도로서,
지반의 함수비(water content)와 공극비(void ratio)의 변화량 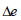 에 의존하는 특성이 있습니다.
지반의 함수비가 클수록 물이 흐를 수 있는 통로의 크기가 커지는 효과로 인하여 포화상태에서 가장
큰 값을 갖고, 함수비는 간극수압에 의존하는 특성이기 때문에 투수계수도 간극수압에 따라 변하게 됩니다.
공극비의 변화는 압밀해석 및 응력-침투 완전 연계 해석에서 고려되며, 공극비의 변화량은 공극비의
초기조건에 대해 계산됩니다. 에 의존하는 특성이 있습니다.
지반의 함수비가 클수록 물이 흐를 수 있는 통로의 크기가 커지는 효과로 인하여 포화상태에서 가장
큰 값을 갖고, 함수비는 간극수압에 의존하는 특성이기 때문에 투수계수도 간극수압에 따라 변하게 됩니다.
공극비의 변화는 압밀해석 및 응력-침투 완전 연계 해석에서 고려되며, 공극비의 변화량은 공극비의
초기조건에 대해 계산됩니다.
midas
GTS NX에서는 간극수압과 공극비의 변화량에 따른 투수계수의 변화를 나타내기 위하여, 포화상태의
투수계수 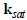 과 간극수압의 변화에 따른 투수계수비 함수 과 간극수압의 변화에 따른 투수계수비 함수 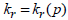 , 공극비의 변화량 , 공극비의 변화량 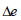 에 따른 투수계수비를
정의하는 에 따른 투수계수비를
정의하는 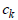 를 사용합니다. 불포화 상태에서 공극비 변화에 따른
투수계수는 다음 식과 같이 구해집니다. 를 사용합니다. 불포화 상태에서 공극비 변화에 따른
투수계수는 다음 식과 같이 구해집니다.
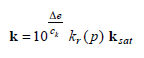
[비저류계수(Ss)]
피압대수층에서
단위 수위강하 혹은 수위상승에 의해 대수층의 단위 부피를 통해 유출되거나 유입되는 물의 부피를 의미합니다.
압축성 유체의 특성을 부여하기 위한 계수로 직접 입력하거나 자동계산할 수 있습니다.
침투
및 압밀해석에서 간극수압에 대한 체적함수비의 변화량은 다음과 같이 간극률과 포화도에 대해 나타낼
수 있습니다.
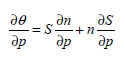
이중
우변의 첫번째 항은 포화조건에서 체적함수비의 기울기를 나타내며, 비저류계수를 사용하여 나타낼 수
있습니다.
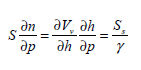
또한,
비저류계수는 재료의 배수특성을 비배수로 설정했을때 비배수 프아송비(vu) 와 일반파라미터에 입력된
유효탄성계수(E') 및 프아송비(v')를 이용하여 자동계산 됩니다.
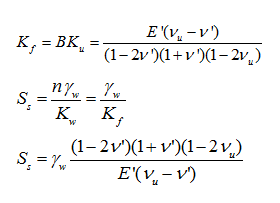
열전도
지반의
투수특성 및 배수/비배수 조건을 정의하는 입력 파라미터와 단위는 아래 테이블과 같습니다.
입력파라미터 |
설명 |
단위 |
전도율 |
열에너지
전도능력 |
J/(m·sec·[T]) |
비열 |
어떤
물질의 1kg을 1°C 올리는데 필요한 열량 |
J/(kN·[T]) |
발열계수 |
발열하중의
scale factor |
- |
부동수분량 |
부동 함수비 |
- |
<열전도 파라미터>
전도율(Conductivity)
: 열에너지를 전도하는 능력을 나타내는 재료의 물성입니다.
비열(Specific
Heat) : 어떤 물질의 1kg을 1°C 올리는데 필요한 열량으로 열전달(과도상태) (Transient
Heat Transfer) 해석시 필수 항목입니다.
발열계수(Heat
Generation Factor) : 열전달해석의 하중벡터로 사용되는 발열하중에 발열계수를 곱한
값이 물체에 가해지는 총 발열 하중 값이 됩니다.
부동수분량(Unfrozen
water content) : soil/rock에서 부동 함수비를 나타냅니다. 지반의 고유특성으로
온도별 함수로 입력받습니다.
콘크리트 크리프 파라미터
콘크리트 구조물의 시간의존 거동을 모사하기 위한 creep
함수를 정의합니다.
점탄성(visco-elastic)
및 점소성(visco-plastic) 재료의 대표적인 거동은 일정한 응력에서 변형률이 증가하는 크리프(Creep)
현상과 일정한 변형률에서 응력이 감소하는 응력이완(Stress Relaxation) 현상으로 나타납니다.
점탄성이란
점성(viscosity)과 탄성을 동시에 가지는 성질을 의미하며, 점소성이란 점성 및 소성 성질을
동시에 가지는 것을 의미합니다. GTS NX에는 점탄성 재료로 재령 독립적(age independent)
모델과 재령 의존적(age dependent) 모델이 있고, 점소성 재료로는 Soft-Soil
Creep 모델이 있습니다.
콘크리트
크리프 적용 가능한 모델은 Elastic,
Tresca, von
Mises, Mohr Coulomb,
Drucker Prager,
Hoek Brown 모델이 있습니다.
[재령
종속]
시간에
따른 크리프 변형은 콘크리트 시편에 일축 단위응력을 콘크리트 재령 τ 에 재하하였을 때, 재령 t
일에서 발생하는 총 변형율을 의미하는 크리프 컴플라이언스(creep compliance), 크리프
함수에서 탄성변형을 제외한 특성 크리프(specific creep), 크리프 함수를 탄성변형과의
비율로 나타낸 크리프 계수(creep coefficient) 로 표현할 수 있습니다.
특정
응력이 작용하는 시간이 다른 경우는 다른 형태의 크리프 함수를 사용하여야 합니다. 따라서, 시간에
따라 응력이 변화하는 경우에 각 시간에서의 증감하는 응력은 독자적인 크리프 함수를 필요로 합니다.
GTS
NX는 aging-Kelvin 크리프 모델과 Kelvin 모델에서 스프링을 제외한 aging-Viscous
모델을 제공합니다.
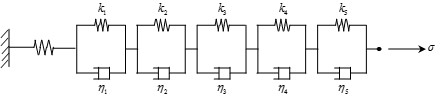
[aging-Kelvin creep model
개념도]
GTS
NX에서는 총 17가지의 크리프/건조수축 함수코드(CEB-FIP(1990), CEB-FIP(1978),
ACI, PCA, Combined(ACI&PCA), AASHTO, European, AS
3600-2009, AS/RTA 5100.5-2011, Russian, Korea Standard,
JAPAN, JAPAN(JSCE), CHINA, China(JTG D62-2004), KCI-USD12,
KSCE 2010, 사용자정의) 및 시간에 따른 12가지 탄성계수 함수코드(CEB-FIP(1990),
CEB-FIB(1978), ACI, Ohzagi, European, AS 3600-2009, AS/RTA
5100.5-2011, Russian, Korea Standard, Japan(Hydration),
Japan(Elasttic), KCI-USD12, 사용자정의) 를 제공합니다.
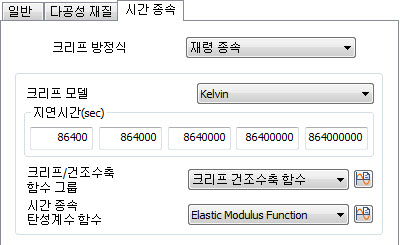
[시간 종속 - 재령 종속]
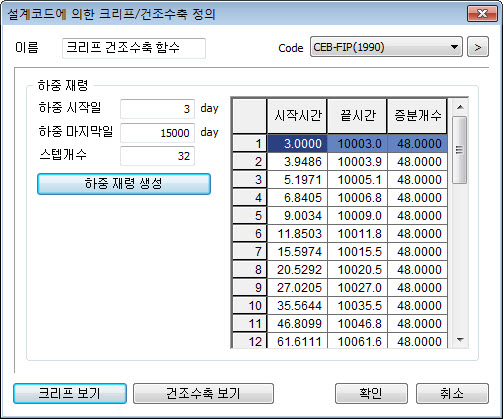
[크리프/건조수축 함수]
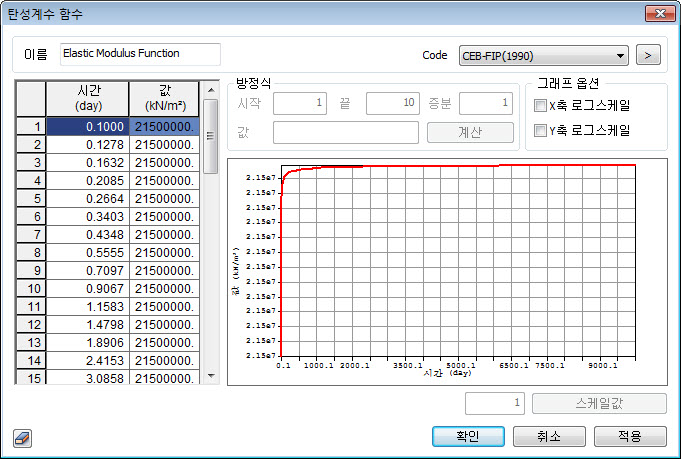
[시간종속 탄성계수 함수]
[재령 독립]
일정한 온도와 응력에서 일축인장시험에서 나타나는 점탄성 재료의 거동은 3가지 영역으로 구분됩니다.
1차 크리프(primary creep)는 시간에 따라 변형률 속도가 감소하는 구간이며, 2차
크리프(secondary creep)는 변형률 속도가 일정한 구간이고, 3차 크리프(tertiary
creep)는 변형률 속도가 증가하는 구간입니다.
GTS NX에서는 등방성 재료에 대해서 1차 크리프와 2차 크리프를 사용할 수 있습니다.
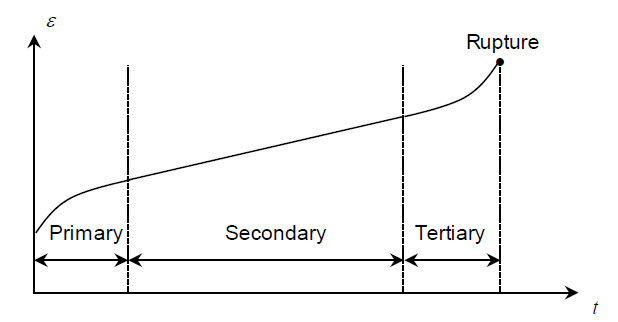
[일정한 온도와 응력에서 일축인장 시험]
만일 크리프 변형이 일어난 이후 작용된 하중이 제거될 경우, 탄성변형은 즉시 회복되고 크리프
변형은 서서히 회복됩니다. 이 대 2차 크리프 변형은 영구 변형으로 남게 됩니다.
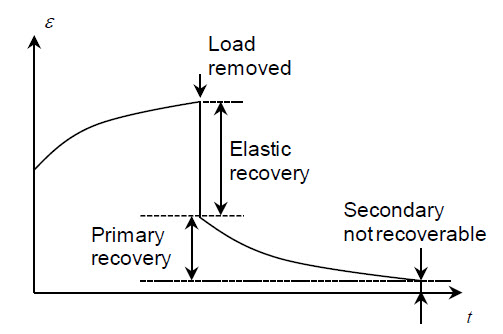
[응력변화에 따른 크리프 변형]
GTS NX에서는 크리프 변형율을 Empirical law 1, Empirical law 2의
두가지 실험식 형태로 정의하거나, 크리프 파라미터를 직접 입력할 수 있습니다.

[Kelvin-Maxwell creep model
개념도]
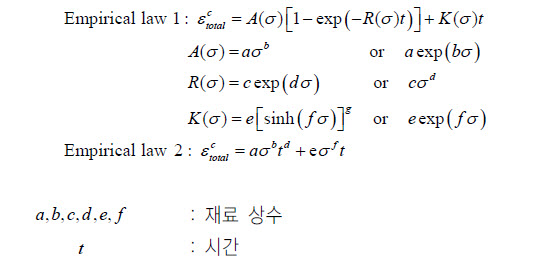
[Emprirical law 수식]
[시간종속- 재령 독립]
|


